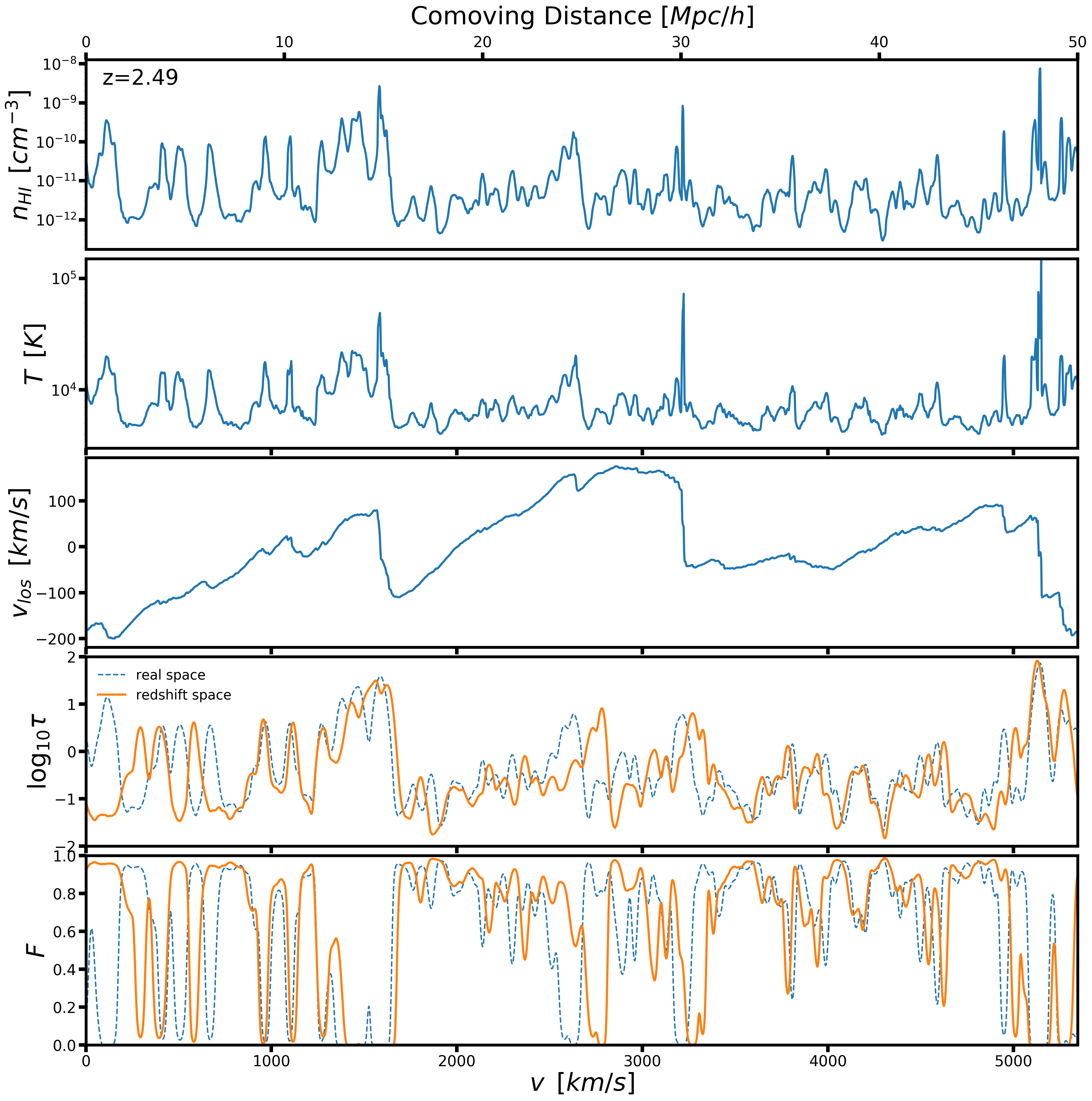
Transmitted Flux
The optical depth \(\tau\) for Ly\(\alpha\) photon scattering is
\[\tau_{v}=\int n_{\mathrm{HI}} \sigma_{v} d r\]where \(v\) is the frequency, \(n_{\mathrm{HI}}\) is the number density of neutral hydrogen, \(\sigma_{v}\) is the cross section of the interaction, and \(dr\) is the proper path length element. Assuming a Doppler line profile, the resulting optical depth is
\[\tau_{v}=\frac{\pi e^{2}}{m_{e} c} f_{12} \int \frac{n_{\mathrm{HI}}}{\Delta v_{D}} \frac{\exp \left[-\left(\frac{v-v_{0}}{\Delta v_{D}}\right)^{2}\right]}{\sqrt{\pi}} d r ,\]where \(\Delta v_{D}= (b/c)v_{0}\) is the Doppler width with the Doppler parameter \(b = b_\mathrm{thermal} = \sqrt{2k_\mathrm{B} T / m_\mathrm{H}}\), and \(f_{12}\) is the upward oscillator strength of the Ly\(\alpha\) resonance transition of frequency \(v_0\).
The path length in the sight line integration is then \(dr = a dx = dv/H\), where \(r\) is the proper distance, \(x\) is the comoving distance, \(v\) is the Hubble flow velocity, and \(H\) is the Hubble expansion rate at that redshift. In velocity coordinates, the optical depth is
\[\tau_{v}=\frac{\pi e^{2} f_{12} \lambda_{0}}{m_{e} c H} \int n_{\mathrm{HI}} \frac{1}{\sqrt{\pi} b} \exp \left[-\left(\frac{v-v_{0}}{b}\right)^{2}\right] d v\]Using the following numerical values:
\(f_{12} = 0.416\), \(\lambda_{\mathrm{Lya}} = 1.21567 \times 10^{-5} \mathrm{cm}\)
Single Absorber
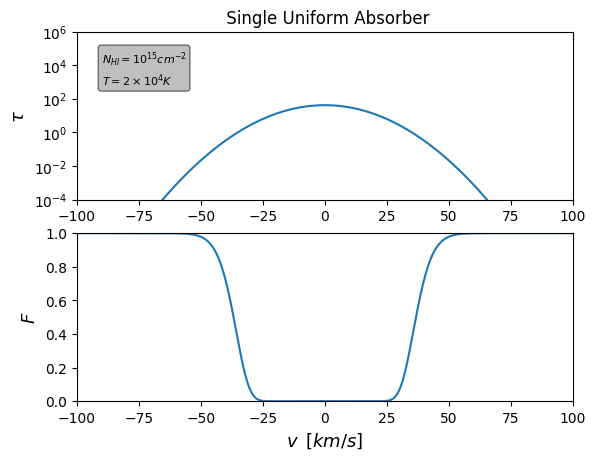
Simulated spectra