Paper Summary: Boera et al. 2019
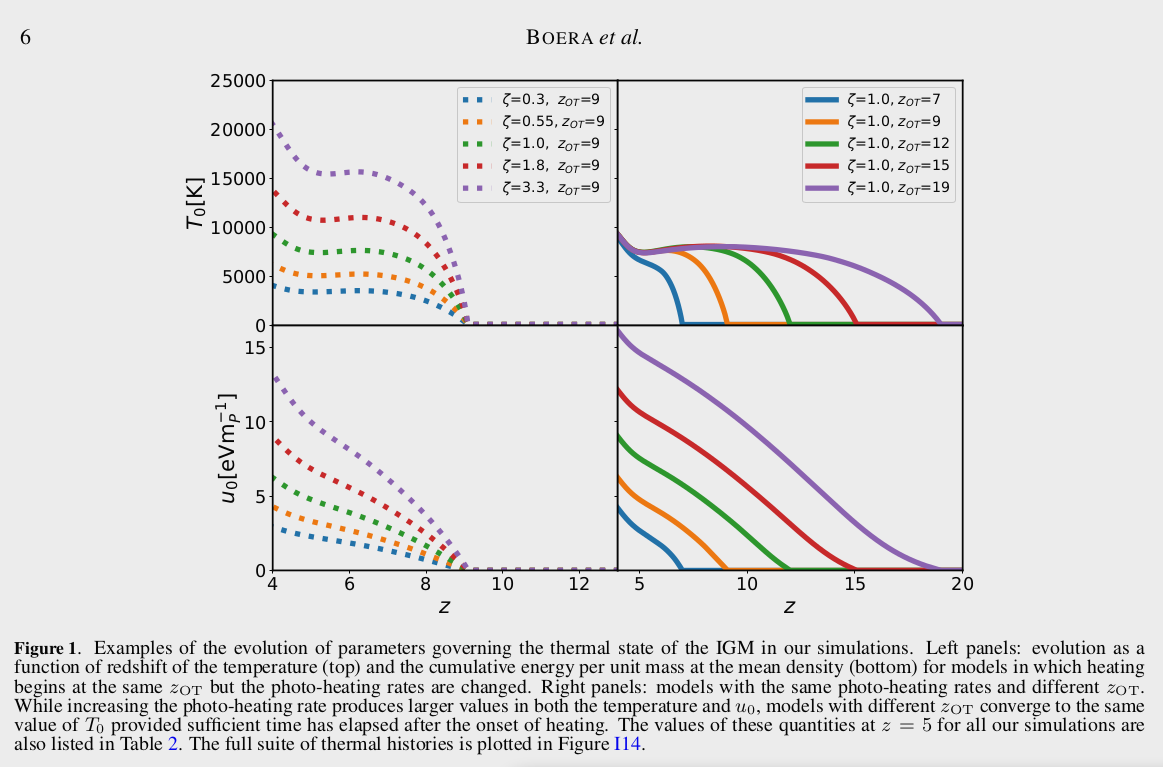
They ran a suite of 30 simulations most of them consist of a 10 Mpc/h box and \(2 \times 512^3\) gas and dark matter particles. The simulations differ on the amplitude of and time of start for the photoheating rates ( they don’t explicitly mention that they also changed the photoionization rates ), they heating rates are just the original HM12 rates multiplied by a constant \(\epsilon_{i}=\zeta \epsilon_{i}^{H M 12}\), where \(\zeta\) takes the following values [ 0.3, 0.55, 1.0, 1.8, 3.3 ], the start redshift for reionization \(z_{OT}\) takes the possible values [ 7, 9, 12, 15, 19 ]. The next figure shows the effect of varying \(\zeta\) and \(z_{OT}\) on \(t_0\) and the integrated integrated heating per unit mass \(u_0\).
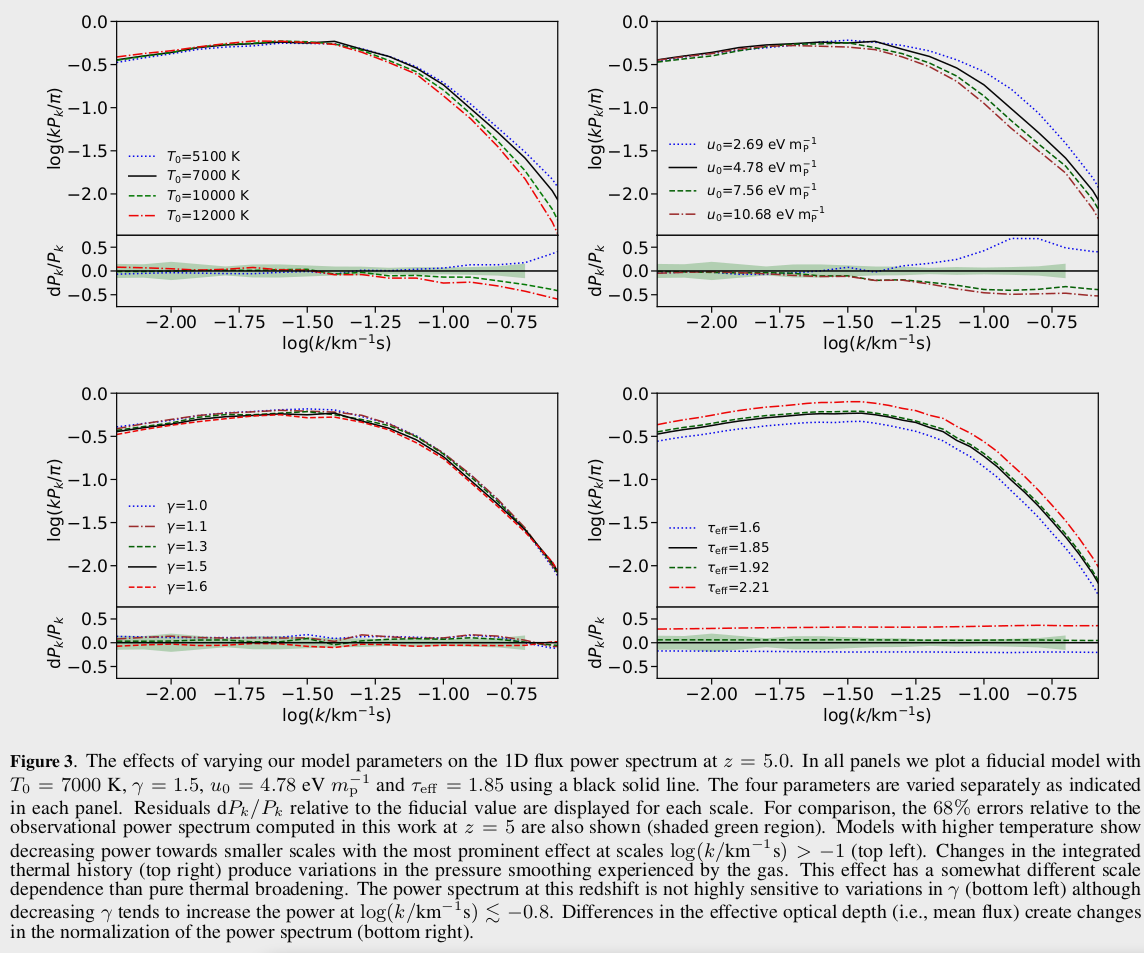
Then they artificially extend their simulation by changing \(T_0\), \(\gamma\), \(\tau_{eff}\), and \(u_0\) as post-processing, the next figure shows the effect that changing this values has on the Flux Power Spectrum.
This is how they change the parameters:
Varying \(T_0\) and \(\gamma\): They rotate and translate the entire \(T-\rho\) plane to match a new \(T_0\) and \(\gamma\)
Varying \(\tau_{eff}\): From what I understand they only changed the Mean Transmitted Flux that they use to normalize the transmitted flux fluctuations for the flux power spectrum, I don’t think they changed the ionization fraction directly.
Varying \(u_0\): Since they ran multiple simulations with different values of \(u_0\), they measure the effect that different \(u_0\) have on the flux power spectrum from their simulations (which they set to have the same \(T_0\), \(\gamma\), and \(\tau_{eff}\) ), from this fit a power law that then they use to get a \(u_0 -P_k\) relation that they can use to sample their MCMC. It seems like they claim to understand the effect that different \(u_0\) have on the power spectrum, so they can artificially change \(P_k\) based on their empirical \(P_k-u_0\) relation, it’s not clear how they take in to account the combined effects of changing the other 3 parameters as well as changing \(u_0\).
Now, they can generate many fake simulations from each real simulation by changing the 4 parameters, it seems to me like they are not interpolating between their real simulations, meaning that the new fake simulations generated from a real one are independent of the other real ones.
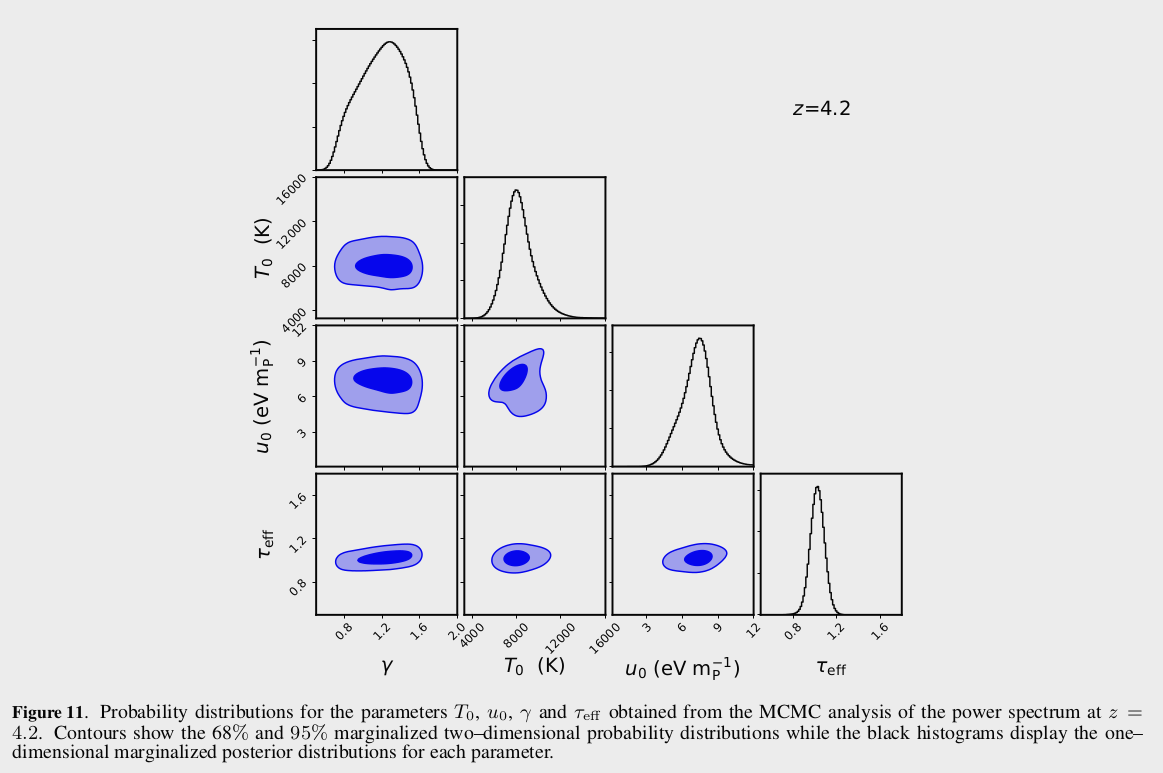
After sampling their MCMC with the new artificial \(P_k\), they measure the constrain values on 4 parameters as shown below for the 3 redshift bins that they constrain from the observed \(P_k\)
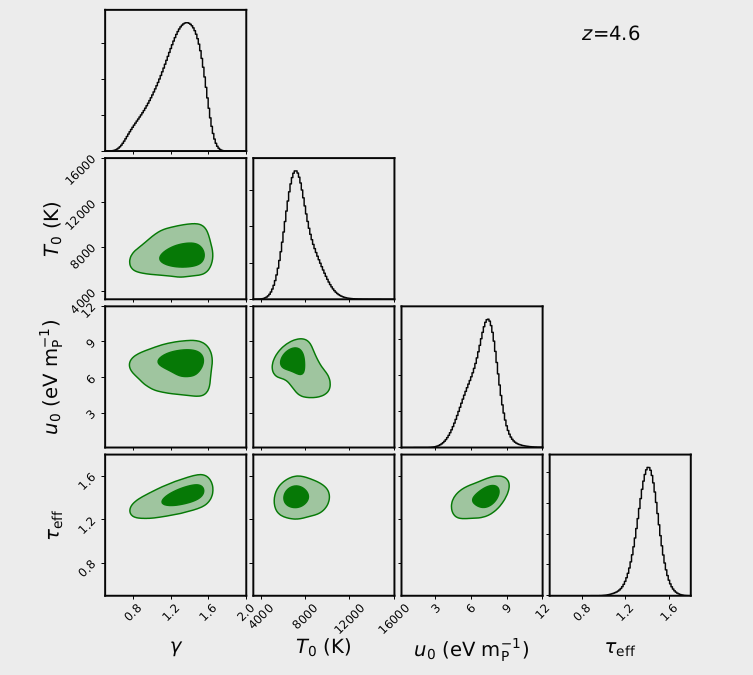
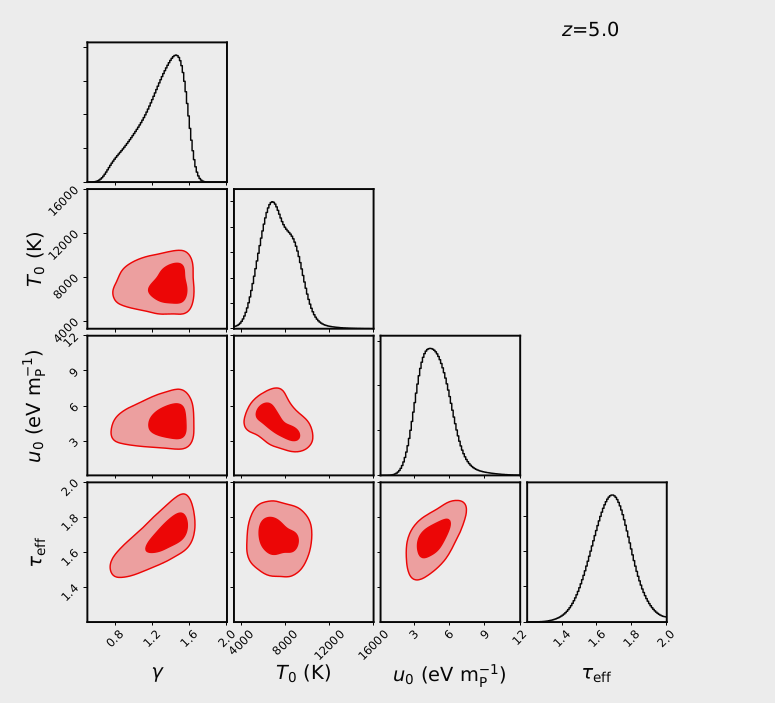
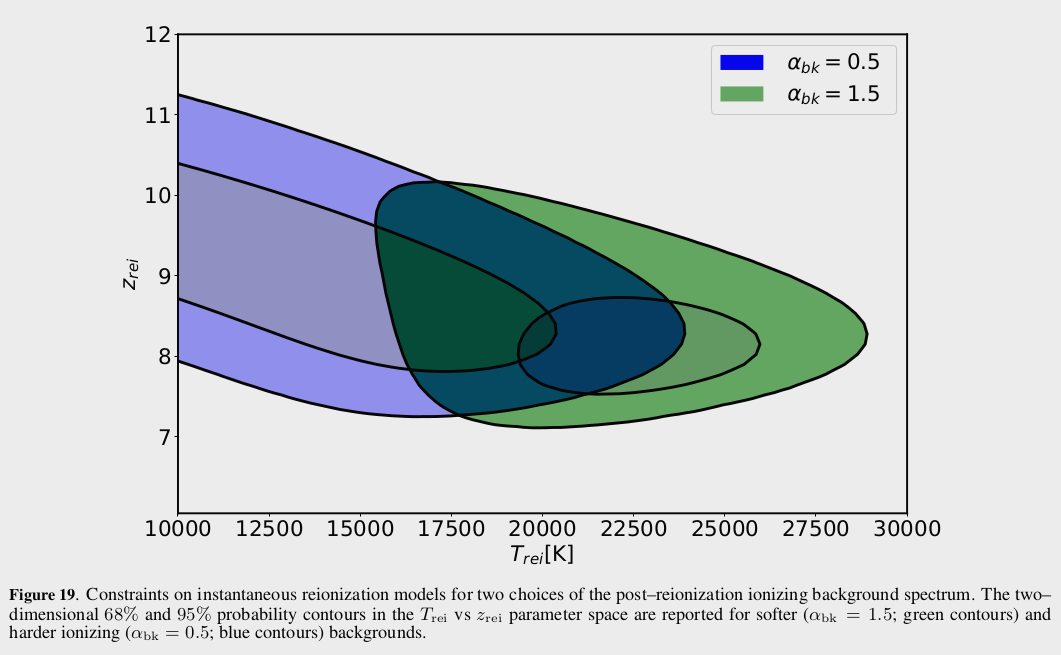
Modeling Instantaneous Reionization
They also model the temperature evolution at mean density, given by:
\[\frac{d T}{d t}=-2 H T+\frac{2 T}{3 \Delta} \frac{d \Delta}{d t}+\frac{2}{3 k_{B} n_{\text {tot }}} \frac{d Q}{d t}\]where:
\[\frac{d Q}{d t}=\sum_{X} \frac{d Q_{p h o t o, X}}{d t}+\frac{d Q_{C o m p t o n}}{d t}+\sum_{i} \sum_{X} R_{i, X} n_{e} n_{X}\]and the injected energy \(u_0\) given by:
\[\frac{d u_{0}}{d t}=\frac{1}{\bar{\rho}} \sum_{X} \frac{d Q_{p h o t o, X}}{d t}\]where:
\[\frac{d Q_{\text {photo}, X}}{d t} \approx \frac{h \nu_{X}}{\gamma_{X}-1+\alpha_{b k}} \alpha_{A, X} n_{\tilde{X}} n_{e}\]by solving for \(T_0\) and \(u_0\) for different Instantaneous reionization histories, where they vary the redshift of reionization \(z_{rei}\), the temperature of reionization \(T_{rei}\) and the spectral index of the ionizing UV Backgroud \(\alpha_{bk}\), the following figure shows the effect that changing each parameter has on the evolution of \(T_0\) and \(u_0\)
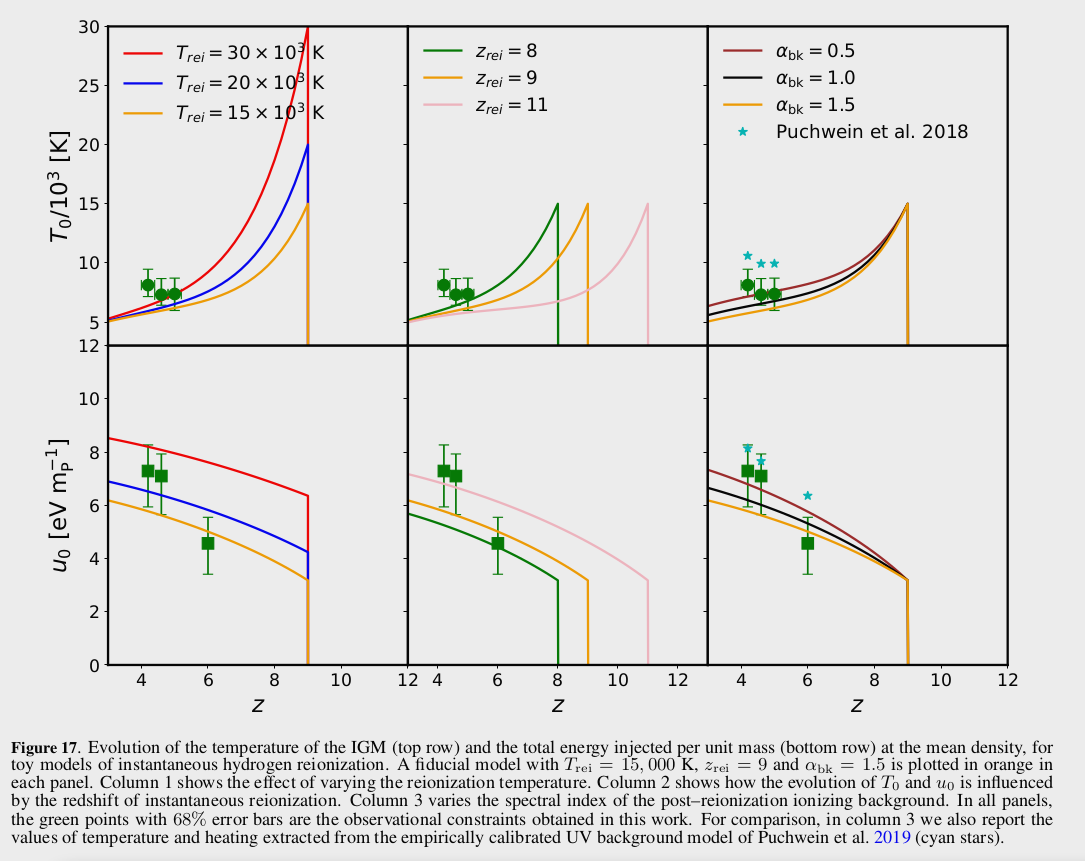
From their \(T_0\) and \(u_0\) measurements they constrain the instant reionization parameters, their results are summarized in the next figure.