ROCKSTAR summary
ROCKSTAR repository Here
ROCKSTAR paper Here
From ROCKSTAR paper:
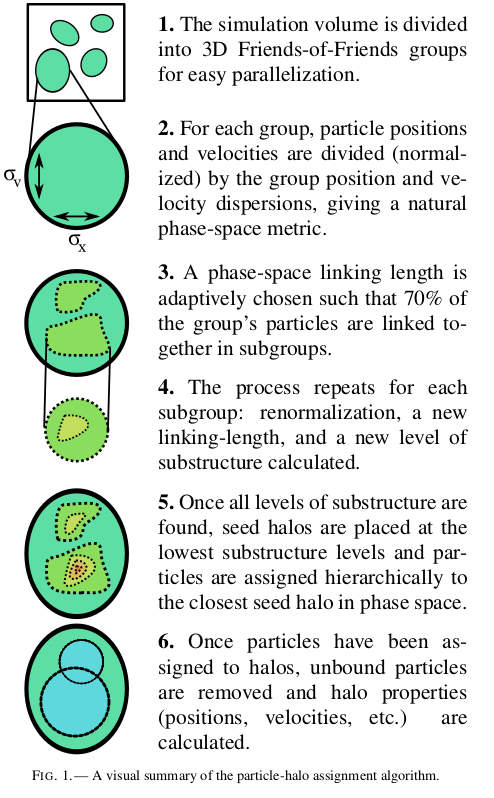
As a first step, our algorithm performs a rapid variant of the 3D friends-of-friends (FOF) method to find overdense regions which are then distributed among processors for analysis. Then, it builds a hierarchy of FOF subgroups in phase space by progressively and adaptively reducing the 6D linking length, so that a tunable fraction of particles are captured at each subgroup as compared to the immediate parent group. Next, it converts this hierarchy of FOF groups into a list of particle memberships for halos.It then computes the host halo/subhalo relationships among halos, using information from the previous timestep if available. Finally, it removes unbound particles from halos and calculates halo properties, before automatically generating particle-based merger trees (§3.5). A visual summary of these steps is shown in Fig. 1.
- Work-Domain decomposition.
Performs a rapid variant of the 3D friends-of-friends (FOF) method to find overdense regions which are then distributed among processors for analysis.
- Finding Halo seeds ( FOF subgroups ).
For each 3D FOF group which is created in the previous step, the algorithm proceeds by building a hierarchy of FOF subgroups in phase space. Deeper levels of subgroups have a tighter linking-length criterion in phase space, which means that deeper levels correspond to increasingly tighter isodensity contours around peaks in the phase-space density distribution. This enables an easy way to distinguish separate substructures — above some threshold phase-space density, their particle distributions must be distinct in phase space; otherwise, it would be difficult to justify the separation into different structures. Beginning with a base FOF group, ROCKSTAR adaptively chooses a phase-space linking length based on the standard deviations of the particle distribution in position and velocity space. That is, for two particles \(p_1\) and \(p_2\) in the base group, the phase-space distance metric is defined as:
\[d( p_{1}, p_{2} ) = \bigg( \frac{ |\vec{x_{1}} - \vec{x_{2}}|^{2} }{\sigma_{x}^2} + \frac{ |v_{1} - v_{2}|^{2} }{\sigma_{v}^2} \bigg)^{1/2}\]where \(\sigma_x\) and \(\sigma_y\) are the particle position and velocity dispersions for the given FOF group; this is identical to the metric of Gottlöber (1998). For each particle, the distance to the nearest neighbor is computed; the phase-space linking length is then chosen such that a constant fraction f (f=0.7) of the particles are linked together with at least one other particle. In large groups (>10,000 particles), where computing the nearest neighbor for all particles can be very costly, the nearest neighbors are only calculated for a random 10,000-particle subset of the group, as this is sufficient to determine the linking length to reasonable precision. Once subgroups have been found in the base FOF group, this process is repeated. For each subgroup, the phase-space metric is recalculated, and a new linking-length is selected such that a fraction f of the subgroup’s particles are linked together into sub-subgroups. Group finding proceeds hierarchically in phase space until a predetermined minimum number of particles remain at the deepest level of the hierarchy. Here we set this minimum number to 10 particles, although halo properties are not robust approaching this minimum.
- Assigning particles to halos.
For each of the subgroups at the deepest level of the FOF hierarchy (corresponding to the local phase-space density maxima), a seed halo is generated. The algorithm then recursively analyzes higher levels of the hierarchy to assign particles to these seed halos until all particles in the original FOF group have been assigned.
For a parent group which contains only a single seed halo, all the particles in the group are assigned to the single seed. For a parent group which contains multiple seed halos, however, particles in the group are assigned to the closest seed halo in phase space. In this case, the phase-space metric is set by the seed halo properties, so that the distance between a halo h and a particle p is defined as:
\[d( h, p ) = \bigg( \frac{ |\vec{x_{h}} - \vec{x_{p}}|^{2} }{r_{dyn}^2 }+ \frac{ |\vec{v_{h}} - \vec{v_{p}}|^{2} }{\sigma_{v}^2} \bigg)^{1/2}\] \[r_{dyn} = \frac{v_{max}}{\sqrt{ \frac{4}{3} \pi G \rho_{vir}}}\]where \(\sigma_v\) is the seed halo’s current velocity dispersion, \(v_{max}\) is its current maximum circular velocity, and “vir” specifies the virial overdensity, using the definition of \(\rho_{vir}\) from Bryan & Norman (1998), which corresponds to 360 times the background density at z = 0, however, other choices of this density can easily be applied. Using the radius \(r_{dyn}\) as the position-space distance normalization may seem unusual at first, but the natural alternative (using \(\sigma_x\) ) gives unstable and nonintuitive results. At fixed phase-space density, subhalos and tidal streams (which have lower velocity dispersions than the host halo) will have larger position-space dispersions than the host halo. Thus, if \(\sigma_x\) were used, particles in the outskirts of a halo could be easily mis-assigned to a subhalo instead of the host halo. Using \(r_{dyn}\) , on the other hand, prevents this problem by ensuring that particles assigned to subhalos cannot be too far from the main density peak even if they are close in velocity space. Intuitively, the largest effect of using \(r_{vir}\) is that velocity-space information becomes the dominant method of distinguishing particle membership when two halos are within each other’s virial radii.
This process of particle assignment assures that substructure masses are calculated correctly independently of the choice of f , the fraction of particles present in each subgroup relative to its parent group. In addition, for a subhalo close to the center of its host halo, it assures that host particles are not mis-assigned to the subhalo — the central particles of the host will naturally be closer in phase space to the true host center than they are to the subhalo’s center.
- Getting substructure.
The most common definition of substructure is a bound halo contained within another, larger halo. Yet, as halo masses are commonly defined to include substructure, the question of which of two halos is the largest (and thus, which should be called a satellite of the other) can change depending on which substructures have been assigned to them. This is one of the largest sources of ambiguity between spherical overdensity halo finders, even those which limit themselves to distinct halos. Break the self-circularity by assigning satellite membership based on phase-space distances before calculating halo masses. Treating each halo center like a particle, we use the same metric as Eq.2 and calculate the distance to all other halos with larger numbers of assigned particles. The satellite halo in question is then assigned to be a subhalo of the closest larger halo within the same 3D friends-of-friends group, ifone exists. If the halo catalog at an earlier timestep is available, this assignment is modified to include temporal information. Halo cores at the current timestep are associated with halos at the previous timestep by finding the halo at the previous timestep with the largest contribution to the current halo core’s particle membership. Then, host-subhalo relationships are checked against the previous timestep; if necessary, the choice of which halo is the host may be switched so as to preserve the host-subhalo relationship of the previous timestep. As explained above, these host-subhalo relationships are only used internally for calculating masses: particles assigned to the host are not counted within the mass of the subhalo, but particles within the subhalo are counted as part of the mass of the host halo. This choice assures that the mass of a halo won’t suddenly change as it crosses the virial radius of a larger halo, and it provides more stable mass definitions in major mergers. Once halo masses have been calculated, the subhalo membership is recalulated according to the standard definition (subhalos are within \(r_\Delta\) of more massive host halos) when the merger trees are constructed. Every density peak within the original FOF analysis group will correspond to either a host halo or a subhalo in the final catalog.
- Unbinding Particles.
By default, ROCKSTAR performs an unbinding procedure before calculating halo mass and \(v_{max}\) , although this may be switched off for studies of e.g., tidal remnants. Because the algorithm operates in phase space, the vast majority of halo particles assigned to central halos are actually bound. We find typical boundedness values of 98% at z = 0. Even for substructure, unbound particles typically correspond to tidal streams at the outskirts of the subhalo, making a complicated unbinding algorithm unnecessary. For this reason, as well as to improve consistency of halo masses across timesteps, we perform only a single-pass unbinding procedure using a modified Barnes-Hut method to accurately calculate particle potentials, the code by default does not output halos where fewer than 50% of the particles are bound; this threshold is user-adjustable, but changing it does not produce statistically significant effects on the clustering or mass function until halos with a bound fraction of less than 15% are included.
- Calculating properties.
**Positions: ** For positions, Knebe et al. (2011) demonstrated that halo finders which calculated halo locations based on the maximum density peak were more accurate than FOF-based halo finders which use the averaged location of all halo particles (see also Gao & White 2006). The reason for this may be simply understood: as particle density rapidly drops in the outer reaches of a halo, the corresponding dispersion of particle positions climbs precipitously. Consequently, rather than increasing the statistical accuracy of the halo center calculation, including the particles at the halo boundary actually reduces it. The highest accuracy is instead achieved when the expected Poisson error (\(\sigma_x / \sqrt{N}\)) is minimized. As our halo finder has access (via the hierarchy of FOF subgroups) to the inner regions of the halo density distribution, an accurate calculation of the center is possible by averaging the particle locations for the inner subgroup which best minimizes the Pois- son error. Typically, for a \(10^6\) particle halo, this estimator ends up averaging the positions of the innermost \(10^3\) particles.
**Velocities: ** The halo core can have a substantial velocity offset from the halo bulk. Since the galaxy hosted by the halo will presumably best track the halo core, we calculate the main velocity for the halo using the average particle velocity within the innermost 10% of the halo radius. For calculating the bound/unbound mass of the halo, however, we use the more appropriate averaged halo bulk velocity including substructure.
**Masses: ** For halo masses, ROCKSTAR calculates spherical overdensities according to multiple user-specified density thresholds: e.g., the virial threshold, from Bryan & Norman (1998), or a density threshold relative to the background or to the critical density. As is usual, these overdensities are calculated using all the particles for all the substructure contained in a halo. On the other hand, subhalo masses have traditionally been a major point of ambiguity (for density-space halo finders). With a phase-space halo finder, such as ROCKSTAR , the particles belonging to the subhalo can be more reliably isolated from the host, and thus less ambiguity exists: the same method of calculating spherical overdensities may be applied to just the particles belonging to the subhalo. In terms of the definition of where the subhalo “ends,” Eq.2 implies that the subhalo edge is effectively where the distribution of its particles in phase space becomes equidistant from the subhalo and its host halo.
Catalog Output:
- Halo masses at several radii: Mvir, M200b, M200c, M500c, M2500c. These masses always include any contributions from substructure. Also, masses with higher density thresholds (e.g., 2500c) can sometimes be zero if the density of the halo never rises above the threshold. [Footnote: Particles are assumed to have an effective radius of FORCE_RES for the purposes of density calculations near the halo center.} By default, only bound particles are included; see Section \ref{s:common_options] if this is not what you want.
- Halo maximum circular velocity and velocity dispersion.
- Halo radii: Rvir and the scale radius r_s, calculated both using profile fitting and using the Klypin v_max method.
- Halo center positions and velocities.
- Halo spin (both Bullock and Peebles) and angular momentum.
- Halo shapes and principal axes, using the Allgood method (iterative, weighted by 1/r^2), at both Rvir and R500c. See Section 2.11.1 for how to change the shape calculation method.
- The ratio of halo kinetic to potential energy, and the center position and velocity offsets from the halo’s bulk average position and velocity.
/* See http://arxiv.org/pdf/astro-ph/0208512v1.pdf */
double _weff(double a)
{
if(a != 1.0)
return W0 + WA - WA*(a - 1.0)/log(a);
else
return W0;
}
double hubble_scaling(double z)
{
double z1 = 1.0+z;
double a = 1.0/z1;
return sqrt(Om * (z1*z1*z1) + Ol*pow(a, -3.0*(1.0 + _weff(a))));
}
double vir_density(double a) {
double x = (Om/pow(a,3))/pow(hubble_scaling(1.0/a-1.0),2.0) - 1.0;
return ((18*M_PI*M_PI + 82.0*x - 39*x*x)/(1.0+x));
}
float _calc_mass_definition(char **md) {
int64_t length = strlen(*md);
char last_char = (length) ? md[0][length-1] : 0;
float matter_fraction = (Om/pow(SCALE_NOW,3))/pow(hubble_scaling(1.0/SCALE_NOW-1.0),2.0);
float cons = Om * CRITICAL_DENSITY / PARTICLE_MASS; // background density
char *mass = *md;
float thresh_dens;
if (mass[0] == 'm' || mass[0] == 'M') mass++;
if (last_char == 'b' || last_char == 'B')
thresh_dens = atof(mass) * cons;
else if (last_char == 'c' || last_char == 'C')
thresh_dens = atof(mass) * cons / matter_fraction;
else {
if (strcasecmp(*md, "vir")) *md = "vir";
thresh_dens = vir_density(SCALE_NOW) * cons;
}
particle_rvir_dens_z0 = vir_density(1.0) * cons;
return thresh_dens;
}
void calc_mass_definition(void) {
char *vir = "vir";
int64_t i;
particle_thresh_dens[0] = _calc_mass_definition(&MASS_DEFINITION);
particle_thresh_dens[1] = _calc_mass_definition(&MASS_DEFINITION2);
particle_thresh_dens[2] = _calc_mass_definition(&MASS_DEFINITION3);
particle_thresh_dens[3] = _calc_mass_definition(&MASS_DEFINITION4);
particle_thresh_dens[4] = _calc_mass_definition(&MASS_DEFINITION5);
particle_rvir_dens = _calc_mass_definition(&vir);
dynamical_time = 1.0/sqrt((4.0*M_PI*Gc/3.0)*particle_rvir_dens*PARTICLE_MASS);
min_dens_index = 0;
for (i=1; i<5; i++)
if (particle_thresh_dens[i] < particle_thresh_dens[min_dens_index])
min_dens_index = i;
}
void _calc_additional_halo_props(struct halo *h, int64_t total_p, int64_t bound)
{
int64_t j, k, part_mdelta=0, num_part=0, np_alt[4] = {0},
np_vir=0, dens_tot=0, parts_avgd = 0, num_part_half = 0;
double dens_thresh = particle_thresh_dens[0]*(4.0*M_PI/3.0);
double d1 = particle_thresh_dens[1]*(4.0*M_PI/3.0);
double d2 = particle_thresh_dens[2]*(4.0*M_PI/3.0);
double d3 = particle_thresh_dens[3]*(4.0*M_PI/3.0);
double d4 = particle_thresh_dens[4]*(4.0*M_PI/3.0);
double rvir_thresh = particle_rvir_dens*(4.0*M_PI/3.0);
double vmax_conv = PARTICLE_MASS/SCALE_NOW;
double r, circ_v, vmax=0, rvmax=0, L[3] = {0}, Jh, m=0, ds;
double vrms[3]={0}, xavg[3]={0}, vavg[3]={0}, mdiff;
double cur_dens, rvir, mvir;
for (j=0; j<total_p; j++) {
if (bound && (po[j].pe < po[j].ke)) continue;
num_part++;
r = sqrt(po[j].r2);
if (r < FORCE_RES) r = FORCE_RES;
cur_dens = ((double)num_part/(r*r*r));
if (cur_dens > dens_thresh) {
part_mdelta = num_part;
dens_tot = j;
}
if (cur_dens > d1) np_alt[0] = num_part;
if (cur_dens > d2) np_alt[1] = num_part;
if (cur_dens > d3) np_alt[2] = num_part;
if (cur_dens > d4) np_alt[3] = num_part;
if (cur_dens > rvir_thresh) {
circ_v = (double)num_part/r;
np_vir = num_part;
if (part_mdelta && circ_v > vmax) {
vmax = circ_v;
rvmax = r;
}
}
}
for (j=0; j<dens_tot; j++) {
if (bound && (po[j].pe < po[j].ke)) continue;
add_ang_mom(L, h->pos, po[j].pos);
parts_avgd++;
if (parts_avgd*2 >= part_mdelta && !num_part_half)
num_part_half = j;
for (k=0; k<3; k++) { //Calculate velocity and position averages
xavg[k] += (po[j].pos[k]-xavg[k])/((double)parts_avgd);
mdiff = po[j].pos[k+3]-vavg[k];
vavg[k] += mdiff/(double)parts_avgd;
vrms[k] += mdiff*(po[j].pos[k+3]-vavg[k]);
}
}
m = part_mdelta*PARTICLE_MASS;
if (!bound) h->m = m;
else h->mgrav = m;
for (k=0; k<3; k++) vrms[k] = (parts_avgd>0) ? (vrms[k]/parts_avgd) : 0;
if ((!bound) == (!BOUND_PROPS)) { //Works even if BOUND_PROPS > 1
h->Xoff = h->Voff = 0;
for (k=0; k<3; k++) {
ds = xavg[k]-h->pos[k]; h->Xoff += ds*ds;
ds = vavg[k]-h->pos[k+3]; h->Voff += ds*ds;
}
h->alt_m[0] = np_alt[0]*PARTICLE_MASS;
h->alt_m[1] = np_alt[1]*PARTICLE_MASS;
h->alt_m[2] = np_alt[2]*PARTICLE_MASS;
h->alt_m[3] = np_alt[3]*PARTICLE_MASS;
h->Xoff = sqrt(h->Xoff)*1e3;
h->Voff = sqrt(h->Voff);
h->vrms = sqrt(vrms[0] + vrms[1] + vrms[2]);
h->vmax = VMAX_CONST*sqrt(vmax*vmax_conv);
h->rvmax = rvmax*1e3;
h->halfmass_radius = sqrt(po[num_part_half].r2)*1e3;
h->r = cbrt((3.0/(4.0*M_PI))*np_alt[2]/particle_thresh_dens[3])*1e3;
calc_shape(h,np_alt[2],bound);
h->b_to_a2 = h->b_to_a;
h->c_to_a2 = h->c_to_a;
memcpy(h->A2, h->A, sizeof(float)*3);
h->r = cbrt((3.0/(4.0*M_PI))*part_mdelta/particle_thresh_dens[0])*1e3;
calc_shape(h,dens_tot,bound);
rvir = cbrt((3.0/(4.0*M_PI))*np_vir/particle_rvir_dens)*1e3;
mvir = np_vir*PARTICLE_MASS;
calc_scale_radius(h, m, h->r, h->vmax, h->rvmax, SCALE_NOW, po, dens_tot, bound);
for (j=0; j<3; j++) h->J[j] = PARTICLE_MASS*SCALE_NOW*L[j];
h->energy = estimate_total_energy(dens_tot, &(h->kin_to_pot));
Jh = PARTICLE_MASS*SCALE_NOW*sqrt(L[0]*L[0] + L[1]*L[1] + L[2]*L[2]);
h->spin = (m>0) ? (Jh * sqrt(fabs(h->energy)) / (Gc*pow(m, 2.5))) : 0;
h->bullock_spin = (m>0) ? (Jh / (mvir*sqrt(2.0*Gc*mvir*rvir*SCALE_NOW/1e3))) : 0;
_calc_pseudo_evolution_masses(h,total_p,bound);
}
}
//Assumes center + velocity already calculated.
void calc_additional_halo_props(struct halo *h) {
int64_t j, total_p;
double dens_thresh;
if (LIGHTCONE) lightcone_set_scale(h->pos);
dens_thresh = particle_thresh_dens[0]*(4.0*M_PI/3.0);
if (h->num_p < 1) return;
total_p = calc_particle_radii(h, h, h->pos, 0, 0, 0);
if (BOUND_OUT_TO_HALO_EDGE) {
qsort(po, total_p, sizeof(struct potential), dist_compare);
for (j=total_p-1; j>=0; j--)
if (j*j / (po[j].r2*po[j].r2*po[j].r2) > dens_thresh*dens_thresh) break;
if (total_p) total_p = j+1;
}
if (total_p>1) compute_potential(po, total_p);
for (j=0; j<total_p; j++)
if (po[j].ke < 0) {
total_p--;
po[j] = po[total_p];
j--;
}
qsort(po, total_p, sizeof(struct potential), dist_compare);
calculate_corevel(h, po, total_p);
if (extra_info[h-halos].sub_of > -1)
compute_kinetic_energy(po, total_p, h->corevel, h->pos);
else
compute_kinetic_energy(po, total_p, h->bulkvel, h->pos);
_calc_additional_halo_props(h, total_p, 0);
_calc_additional_halo_props(h, total_p, 1);
if (analyze_halo_generic != NULL) analyze_halo_generic(h, po, total_p);
}
From previous code blocks \(M_{vir}\) is calculated using bound particles in the next steps:
//From file: config.template.h
'string(MASS_DEFINITION, "vir"); //vir is the default MASS_DEFINITION
particle_thresh_dens[0] = _calc_mass_definition(&MASS_DEFINITION);
dens_thresh = particle_thresh_dens[0]*(4.0*M_PI/3.0);
\\ Get M_vir using bound paricles
_calc_additional_halo_props(h, total_p, 1)
\\\\\\\\\\\\\\\\\\\\\\\\\
particle_rvir_dens = _calc_mass_definition(&vir);
cons = Om * CRITICAL_DENSITY / PARTICLE_MASS; // background density
particle_rvir_dens = vir_density(SCALE_NOW) * cons;
rvir_thresh = particle_rvir_dens*(4.0*M_PI/3.0);
for (j=0; j<total_p; j++) {
if (bound && (po[j].pe < po[j].ke)) continue;
num_part++;
r = sqrt(po[j].r2);
if (r < FORCE_RES) r = FORCE_RES;
cur_dens = ((double)num_part/(r*r*r));
if (cur_dens > dens_thresh) {
part_mdelta = num_part;
dens_tot = j;
}
if (cur_dens > rvir_thresh) {
circ_v = (double)num_part/r;
np_vir = num_part;
if (part_mdelta && circ_v > vmax) {
vmax = circ_v;
rvmax = r;
}
}
m = part_mdelta*PARTICLE_MASS;
if (!bound) h->m = m;
else h->mgrav = m;
h->r = cbrt((3.0/(4.0*M_PI))*part_mdelta/particle_thresh_dens[0])*1e3;
\\ In the catalogs mbound_vir is outputed using h->mgrav
\\ and rvir is is outputed using h->r
}