WFIRST Simulation parameters
Parameters used for Millenium simulations Here
Softening From Power et al 2003 numerical convergence criteria, in order to get a well resolved halo:
\[\epsilon_{opt} \, = \, \frac{4r_{200}}{\sqrt{N_{200}}}\]The size of the box is 115 Mpc/h
| \(N_{part}\) | \(\epsilon\) [kpc/h] |
|---|---|
| \(128^3\) | 19.41 |
| \(256^3\) | 9.70 |
| \(512^3\) | 4.85 |
| \(1024^3\) | 2.42 |
| \(2048^3\) | 1.21 |
| \(4096^3\) | 0.61 |
Results for \(256^3\) simulation using \(\epsilon=9.7\):
Gadget parameter file HERE
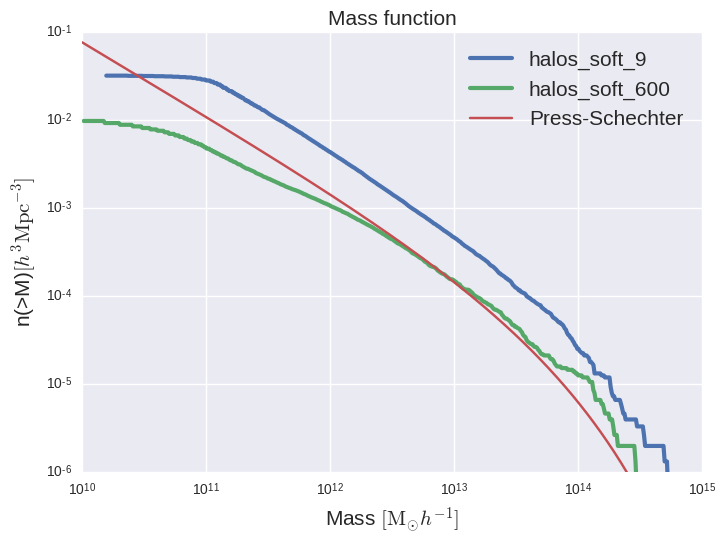

Density projection for \(\epsilon=600\):

From Gadget_guide:
Gravity is softened with a spline, as outlined in the code paper. The softenings quoted here all refer to \(\epsilon\), the roughly equivalent Plummer softening length. Note that for the spline that is actually used, the force will be exactly Newtonian beyond h = 2.8\(\epsilon\). The softening lengths are in internal length units. For comoving integration, the softening refers to the one employed in comoving coordinates, which usually stays fixed during the simulation. However, employing the MaxPhys parameters described below the code can also be asked to switch to a fixed softening in physical scale below a certain redshift.
In cosmological simulations, one sometimes wants to start a simulation with a softening \(\epsilon_{com}\) that is fixed in comoving coordinates (where the physical softening, \(\epsilon_{phys} = a \epsilon_{com}\) , then grows proportional to the scale factor, but at a certain redshift one wants to freeze the resulting growth of the physical softening \(\epsilon_{maxPhys}\) at a maximum value. These maximum softening lengths are specified by the SofteningMaxPhys parameters. In the actual implementation, the code uses \(\epsilon'_{com} = min(\epsilon_{com} , \epsilon_{maxPhys} /a)\) as comoving softening.