The simulations are \(128^3\) and 50Mpc.

Dual Energy Parameters: \(\eta=0.005\) \(\beta_0 = 0.25\) \(\beta_1 = 0.0\)

Shock Detection

Pressure Jump:

From Fryxell 200 the Pressure Jump Condition for shock detection is:

\[\frac{\left|\langle P\rangle_{i+1}^{n}-\langle P\rangle_{i-1}^{n}\right|}{\min \left(\langle P\rangle_{i+1}^{n},\langle P\rangle_{i-1}^{n}\right)}> \alpha \gamma \frac{\left|\langle\rho\rangle_{i+1}^{n}-\langle\rho\rangle_{i-1}^{n}\right|}{\min \left(\langle\rho\rangle_{i+1}^{n},\langle\rho\rangle_{i-1}^{n}\right)}\]

Their implementation uses \(\alpha = 0.1\)

To ignore fluctuations due to noise a condition in the density is also applied:

\[\frac{\left|\langle\rho\rangle_{i+1}^{n}-\langle\rho\rangle_{i-1}^{n}\right|}{\min \left(\langle\rho\rangle_{i+1}^{n},\langle\rho\rangle_{i-1}^{n}\right)}<0.01\]

Phase Diagram

Row 1: Without Pressure Jump Condition

Now Using Pressure Jump condition:

Row 2: Using \(\alpha=0.1\)

Now only using the Total Internal Energy if \(U_{total} > U_{advected}\)

Row 3: Using \(\alpha=1.0\)

Row 4: Using \(\alpha=10.0\)

Chemistry Projection

No Pressure Jump Condition

Using Pressure Jump Condition \(\alpha=10.0\)

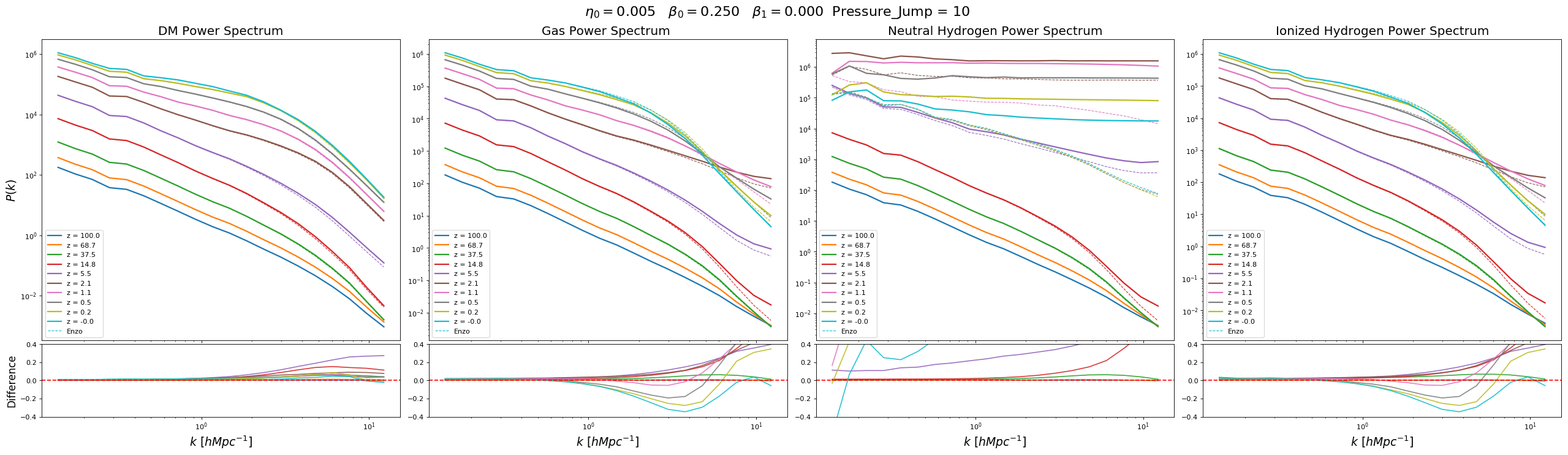
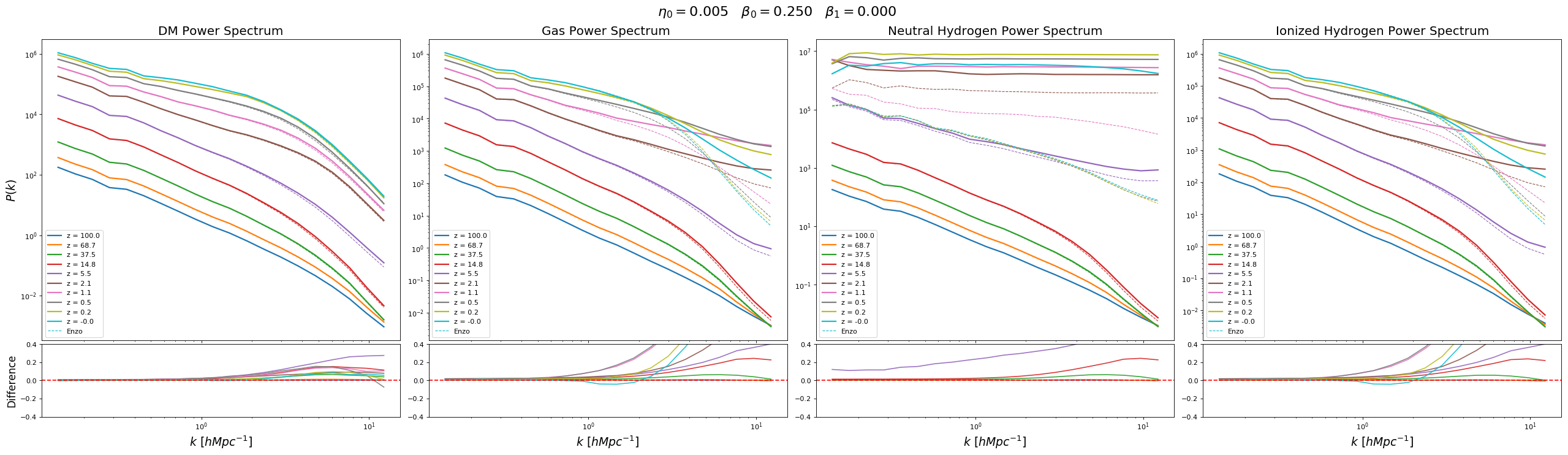
Power Spectrum

No Pressure Jump Condition

Using Pressure Jump Condition \(\alpha=10.0\)