CHOLLA_PM: Dual energy: error cells
Column 1: ENZO
Column 2: Phase diagram for All Gas ( top ) and Neutral Hydrogen ( bottom ). Temperature is internally computed by Grackle on run time.
Column 3: Phase diagram for the fraction of the gas that uses the Total Internal Energy to compute pressure.
Column 4: Phase diagram for the fraction of the gas that uses the Adavected Internal Energy to compute pressure.
Column 5: Phase diagram showing the temperature computed from the Total Internal Energy for ALL the gas.
Column 6: Phase diagram showing the temperature computed from the Advected Internal Energy for ALL the gas.
First I limit the max fractional change of the advected internal energy to 0.5, the comparison is below, the first row is the evolution without restricting the max change and the second row is limiting the max change.
Now I track the first 5 cells to hit the temperature floor, here are their last steps ( cells marked in red ):
From the last snapshots I get the Advected Internal Energy ( U_advected ). also I write the change in Internal energy corresponding to the Advection term ( \(\Delta\) advc_term ) and the change due to the divergence of the velocity ( \(\Delta\) P Div(v) ).
The values as a function of time are shown below:
\[( U + \Delta )^n = U^{n-1} + \Delta^{n-1}\]The blue line corresponds to the temperature in logarithmic scale.
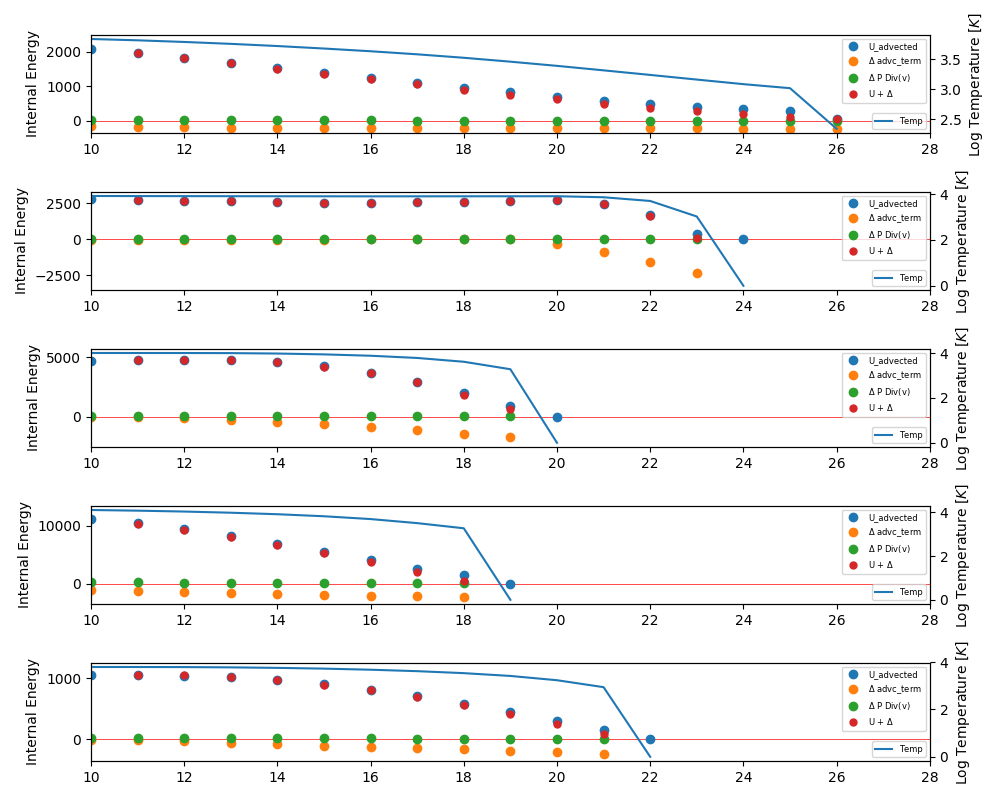
The change due to the divergence term is always positive!, this means that this term is heating the gas.
The Conclusion is that the divergence term is not causing the cooling of the gas, the error is coming from the advection term. Previously we saw that without the Div(v) term the advection was correct, could it be that during that idealized test in which the temperature remains uniform the pressure gradients are low so that we don’t see errors comming from the advection term.
Here is the evolution of the advected Internal Energy without the divergence term on the integration, the same cells fall to the floor at the same time.
Here is the evolution using PCM for the reconstruction, the low temperature deviations are gone!
Now the gas is heating too much, the conclusion is that the reconstruction scheme we used PPMC is either inappropriate for this conditions or the implementation is incorrect, I find very suspicious that the advection term is lowering the advected internal energy so much but not the density.