In order to test the self-gravity implementation in CHOLLA, I ran a \(512^3\) adiabatic simulation of an ideal gas \((\gamma = 5/3)\) collapsing under it’s own gravity.

The box size is \(L=1\), the density in the box is \(\rho=0.1\) and for the spherical region of \(R < 0.2\) there is an over-density of \(\rho=1\). Initial velocities are uniform \(v=0\) and pressure is uniform \(p=0.001\).

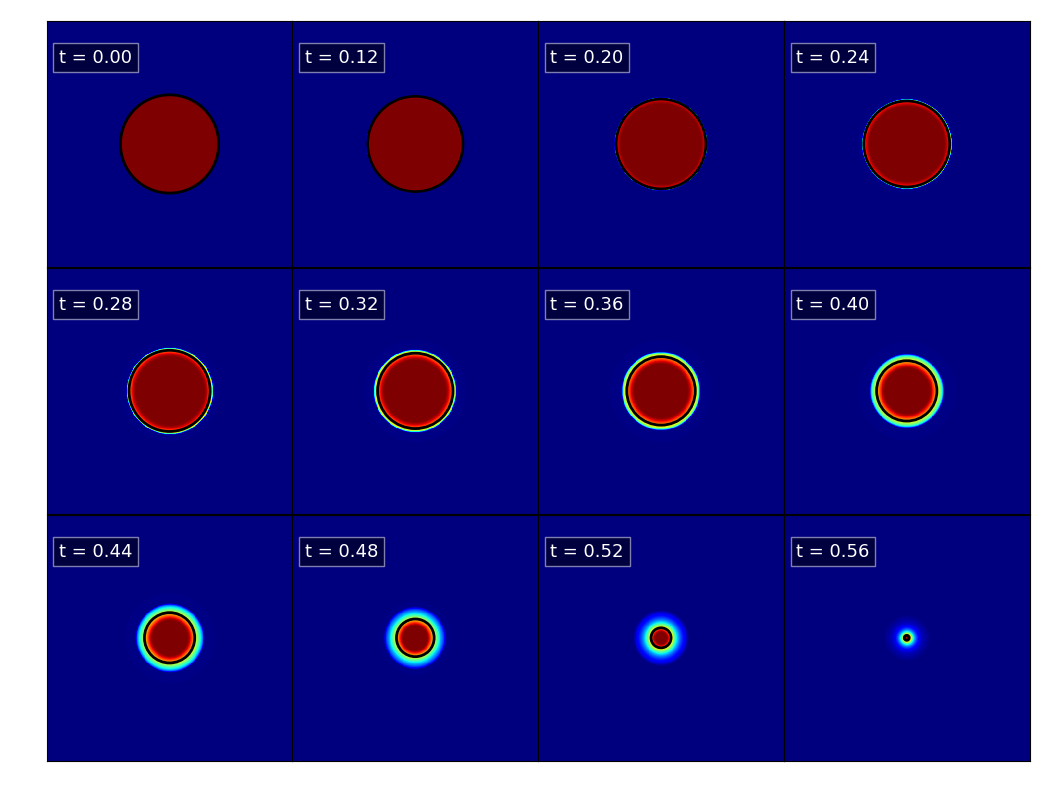
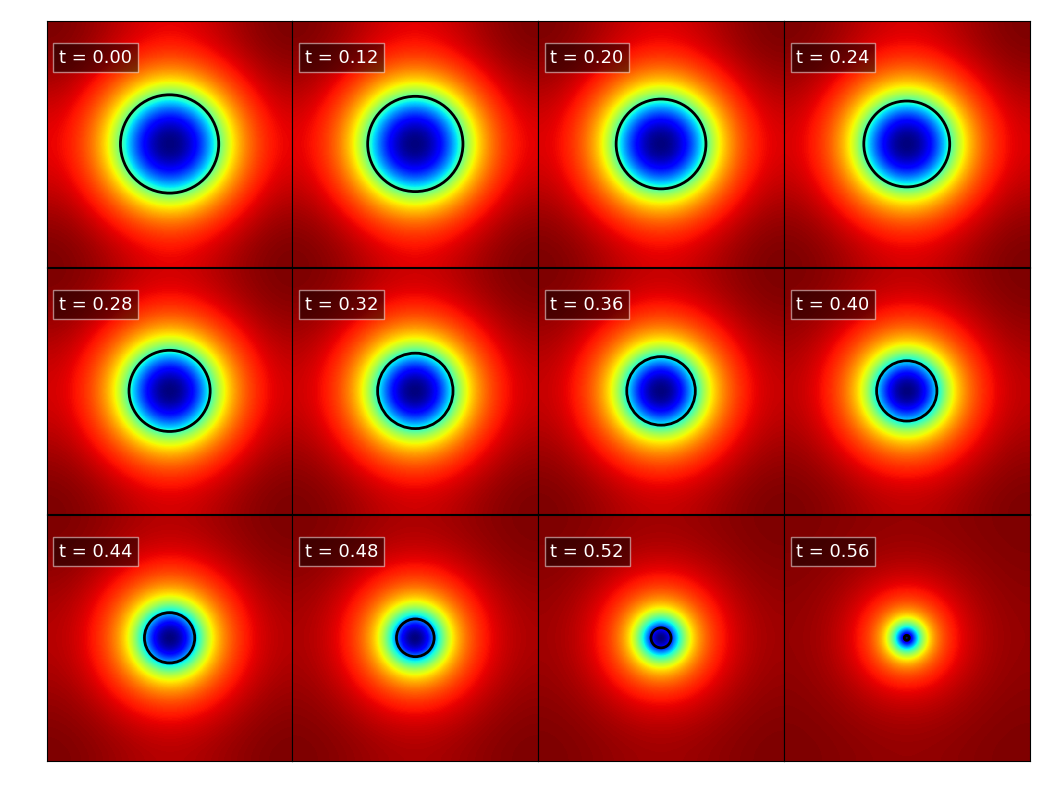
The next figures show density and potential center slices. The black circle corresponds to the analytical value for the radius of a uniform pressure-less system collapsing only under gravity.

Density

Potential

Timing for several grid configurations

All times are in seconds and correspond to the average of the first 20 time-steps ( not counting the first two time-steps )

nGPUs nx ny nz time_hydro time_potential time_boundaries
8 256 256 256 0.613 0.689 0.275
16 512 256 256 0.691 0.762 0.339
32 512 512 256 0.818 1.513 0.939
64 512 512 512 0.869 1.972 1.361
128 1024 512 512 0.932 2.121 1.592

For the XSTREAM system there was no debug queue, this makes any development to be very tedious, and I wasn’t able to run more than 128 GPUs.

NOTE: This was the implementation of the poisson solver that wasn’t optimized for solving real-complex-real FFTs, also there was another optimization that avoided the last transposition for the forward FFT saving communication time.