Physical mean Internal Energy for early redshift

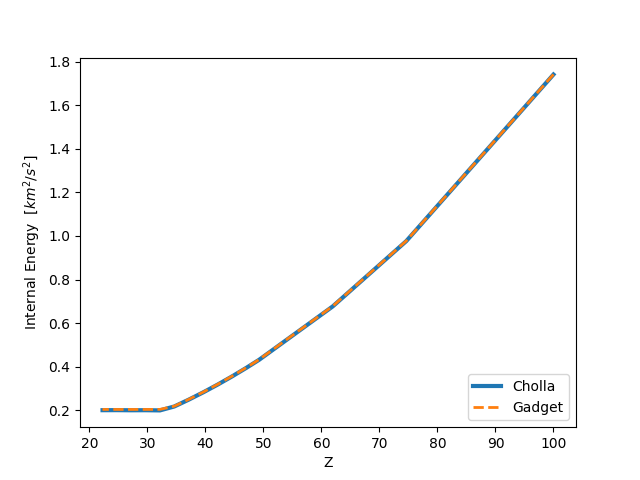
CASE 1: Zero initial velocities, no gravity acting on the gas

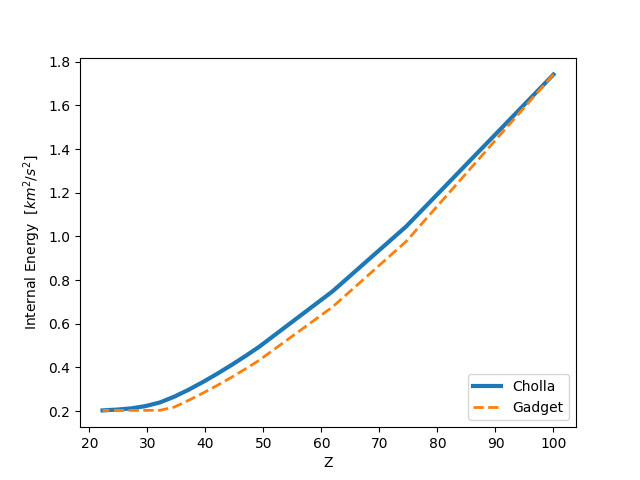
CASE 2: Initial velocities, NO gravity acting on the gas

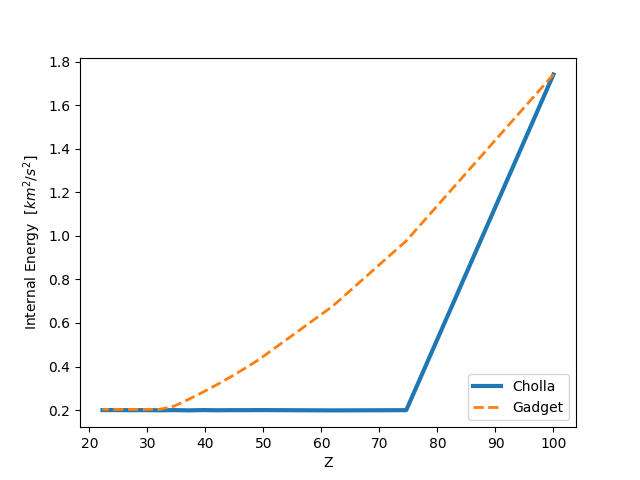
CASE 3: Initial velocities, Now gravity is acting on the gas, and the gas cools very fast.

From Initial Conditions

Dens mean: 13.4874

U mean: 0.00017072 \(km^2/s^2\)

Ek mean: 0.15950561 \(km^2/s^2\)

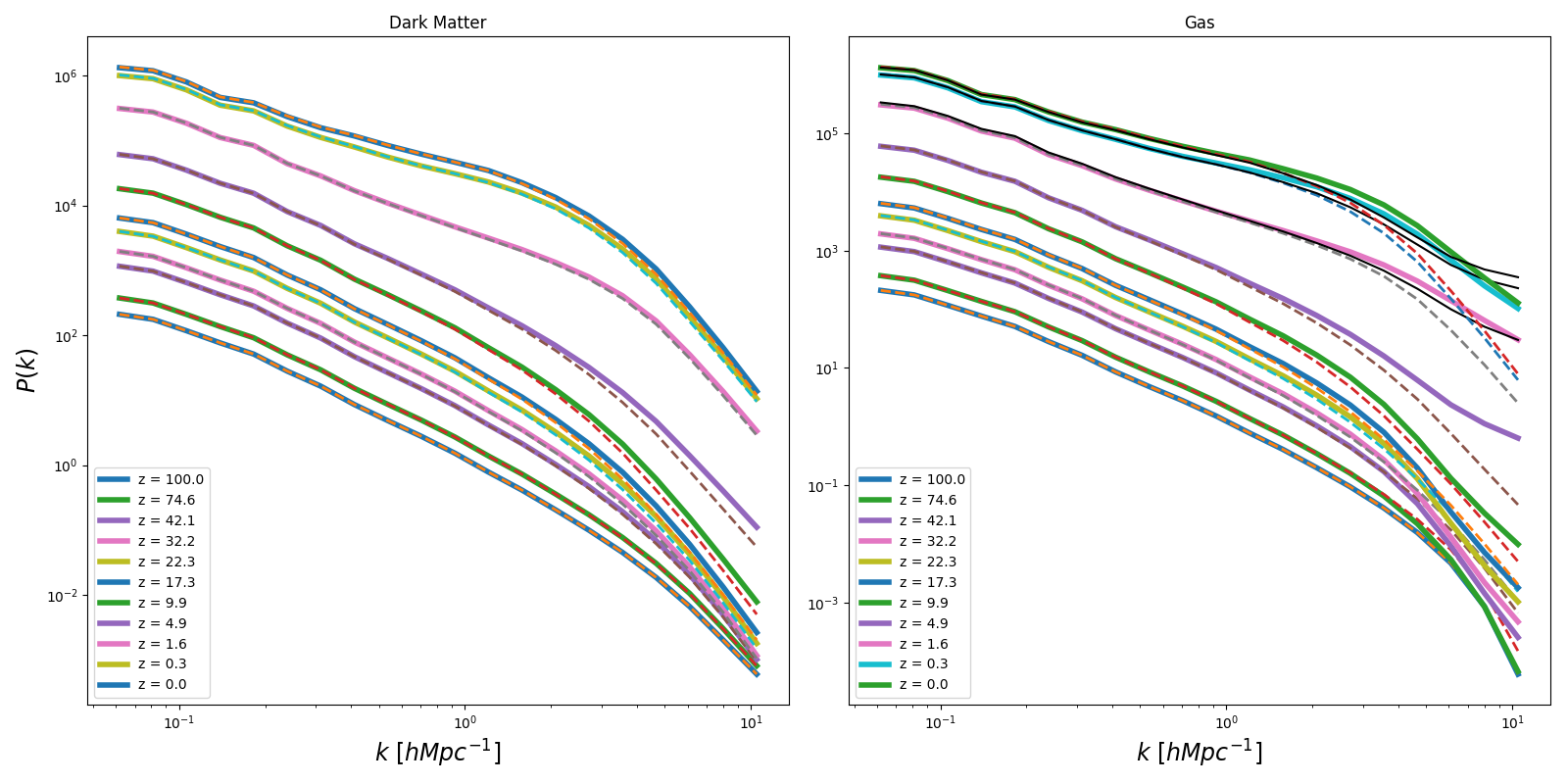
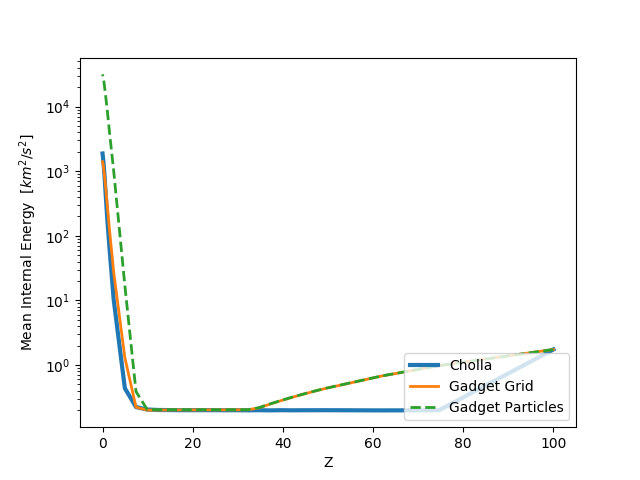
Physical mean Internal Energy for the entire simulation

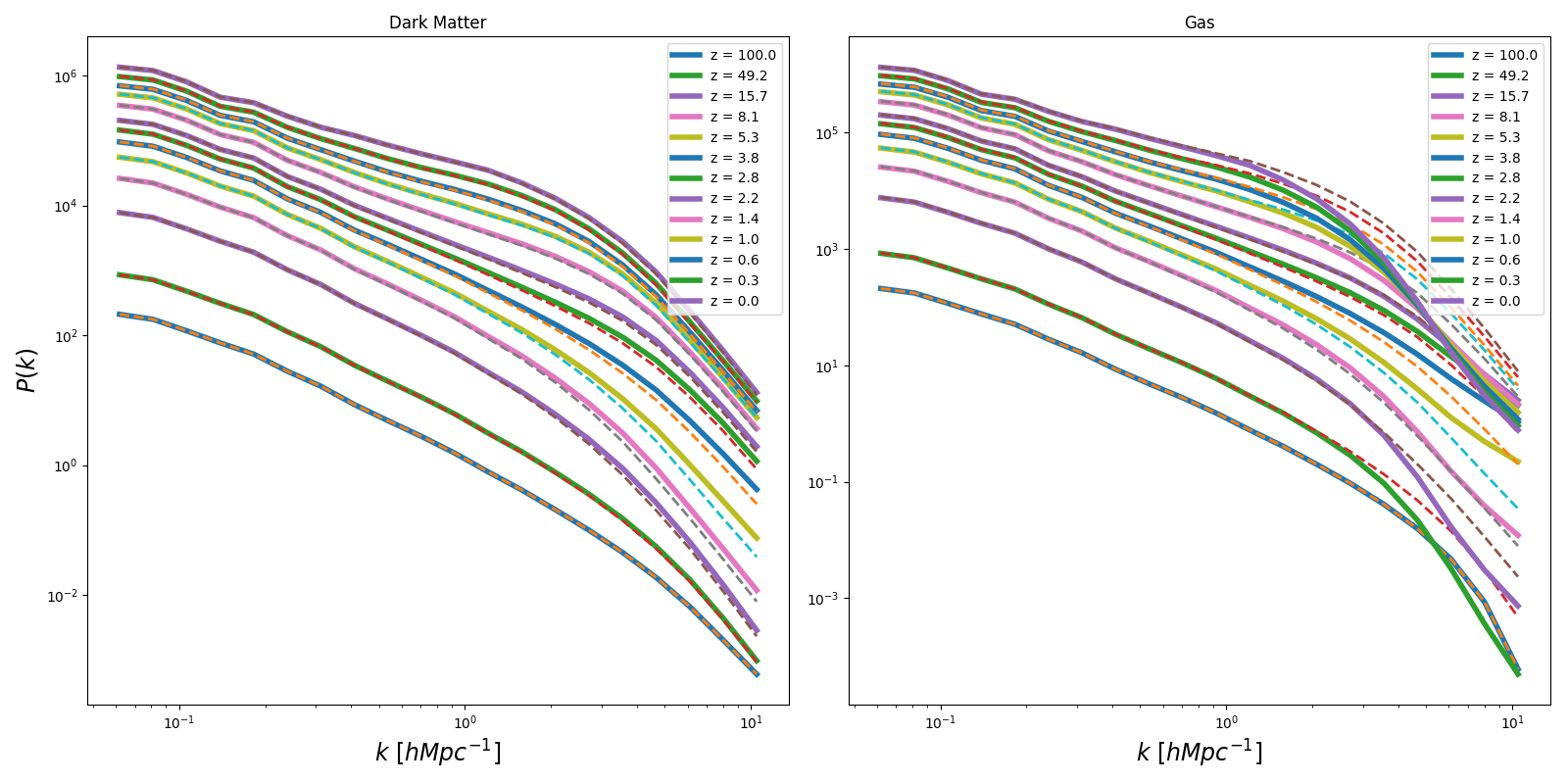
Density Power Spectrum (update)

PREVIOUS: For this case the gravitational force acting on the Kinetic Energy of the gas was computed from the Virtual Work done by the gravitational force \(\Delta E = dt (-\rho \nabla \phi \cdot \overrightarrow{v})\)

NOW: Instead of using the virtual work, I compute the change in momentum and use it to compute the change in Kinetic Energy \(\Delta E= dt( \Delta (P^2) / ( 2\rho ) )\)