Flux calculation: Velocity gradient REVISED

The equation using Hubble velocity along the line of sight to do the integral:

$\tau_{u_{0}}=\frac{\pi e^{2} \lambda_{0}}{m_{e} c } f_{12} \int \frac{n_{\mathrm{HI}}}{\sqrt{\pi} b} \exp \left[-\left(\frac{u-u_{0}}{b}\right)^{2}\right] \frac{1}{H} \, dv$, where $dv = H dr$ is the differential in Hubble velocity along the LOS

For the second form of the equation, using the gas velocity $Hr + u_\mathrm{pec}$ to do the integral, then

$$dr = \left| \frac{du}{dr} \right| ^{-1} du = \left| \frac{1}{ H + \nabla u_\mathrm{pec}} \right| du$$

Where

$$du = \left| H dr + \Delta u_\mathrm{pec} \right|$$

is the differential of the gas velocity along the LOS. Note that an absolute value around $du$ is needed to avoid negative values.

$$\tau_{u_{0}}=\frac{\pi e^{2} \lambda_{0}}{m_{e} c } f_{12} \int \frac{n_{\mathrm{HI}}}{\sqrt{\pi} b} \exp \left[-\left(\frac{u-u_{0}}{b}\right)^{2}\right] \left|\frac{1}{ H + \nabla u_\mathrm{pec}} \right| d u$$

Numerically the gradient and the difference are evaluated:

$$\nabla u_\mathrm{pec} = \frac{u_\mathrm{pec}^{i+1} - u_\mathrm{pec}^{i-1} }{2 dr}$$ $$\Delta u_\mathrm{pec} = \frac{u_\mathrm{pec}^{i+1} - u_\mathrm{pec}^{i-1} }{2 }$$

The comparison of the Flux from the two calculations is below.

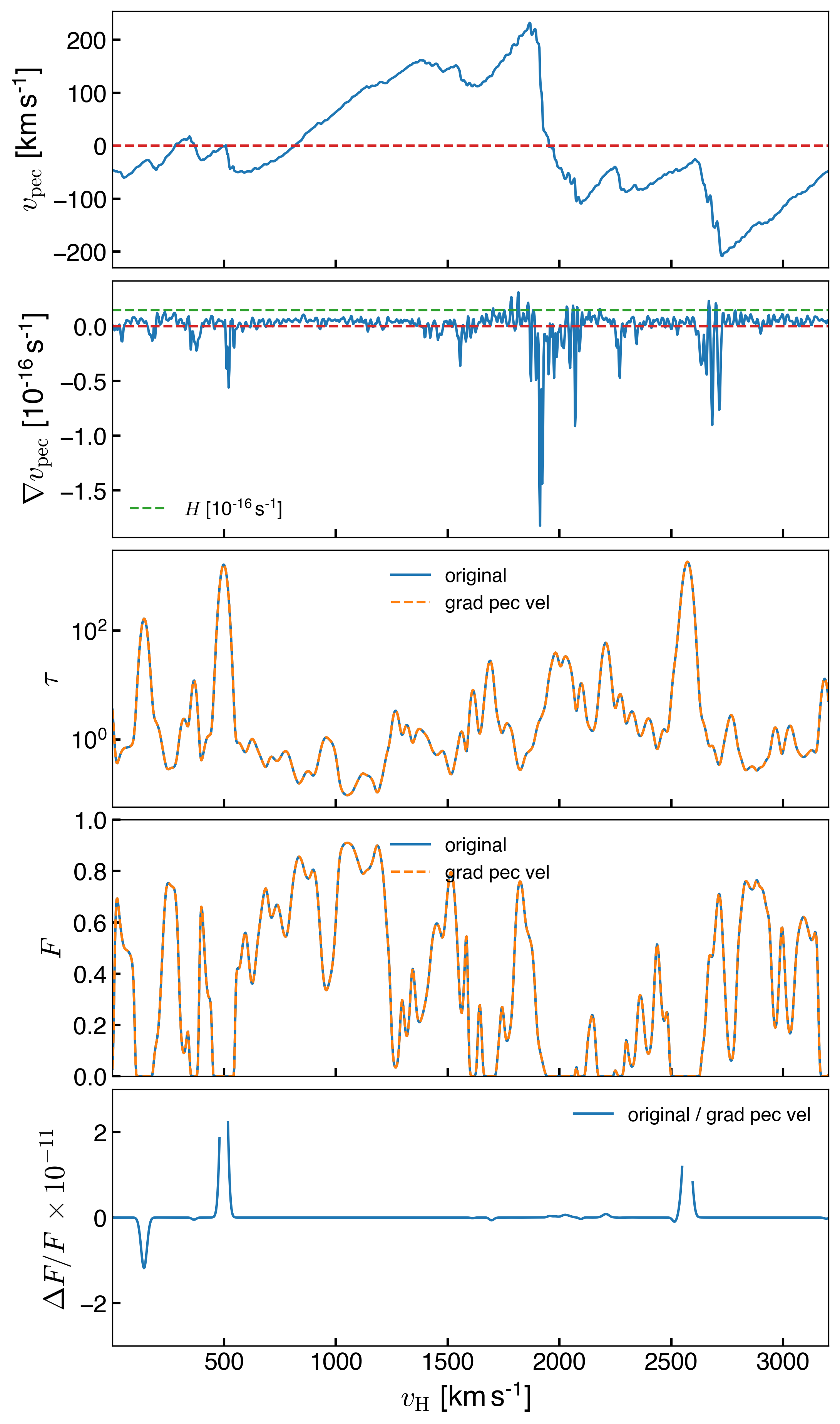
The fractional differences in the Flux are $\lesssim 10^{-11}$!!!

Actually, the term

$$\frac{H dr + \Delta u_\mathrm{pec}}{ H + \nabla u_\mathrm{pec}} = \frac{H dr + \Delta u_\mathrm{pec}}{ H + \frac{\Delta u_\mathrm{pec}}{dr}} = dr \frac{H + \frac{\Delta u_\mathrm{pec}}{r}}{ H + \frac{\Delta u_\mathrm{pec}} {dr}} = dr$$

Which of course should hold from the Jacobian of the transformation. Then this becomes the original form of the equation just changing $dr = H^{-1} dv$

The issue that I had before was that I was missing the term $\Delta u_\mathrm{pec}$ in $du$.