Flux calculation: Velocity gradient
Original equation for optical depth (Gaussian profile):
\[\tau_{\nu_{0}}=\frac{\pi e^{2}}{m_{e} c} f_{12} \int \frac{n_{\mathrm{HI}}}{\sqrt{\pi} \Delta \nu_{\mathrm{D}}} \exp \left[-\left(\frac{\nu-\nu_{0}}{\Delta \nu_{\mathrm{D}}}\right)^{2}\right] d r\]Transform the integral from physical space to velocity space:
\[\tau_{u_{0}}=\frac{\pi e^{2} \lambda_{0}}{m_{e} c } f_{12} \int \frac{n_{\mathrm{HI}}}{\sqrt{\pi} b} \exp \left[-\left(\frac{u-u_{0}}{b}\right)^{2}\right] \left(\frac{du}{dr} \right)^{-1} d u\]In the Russian paper they use the absolute value of \(du/dr\) instead ( I don’t understand why, perhaps my calculus is rusty). The te equation is written:
\[\tau_{u_{0}}=\frac{\pi e^{2} \lambda_{0}}{m_{e} c } f_{12} \int \frac{n_{\mathrm{HI}}}{\sqrt{\pi} b} \exp \left[-\left(\frac{u-u_{0}}{b}\right)^{2}\right] \left|\frac{du}{dr} \right|^{-1} d u\]Which of the following is the correct version for the derivative inside the integral?
\[\left|\frac{du}{dr} \right| = H\]or
\[\left|\frac{du}{dr} \right| = H + \nabla v_\mathrm{pec}(r)\]If the second version (including) the gradient of \(v_\mathrm{pec}\) is the correct one. Would you get the same optical depth when using the equation in frequency space (integrating over \(r\)) and when using the equation in velocity space? I don’t think so. There is no gradient in frequency space and the transformation from frequency to velocity is linear (Doppler).
I believe the correct answer is that when taking the equation which integrates over physical space (\(dr\)) to make the transformation and integrate over velocity space one switches to integrate over the physical coordinate along the line of sight to the velocity coordinate along the line of sight. To go from position to velocity along the line of sight the relation is \(v = H\,r\), I don’t understand why would you include the peculiar velocity of the gas when transforming to velocity coordinate?
I suspect the the Russian version of the equation is the one that is incorrect.
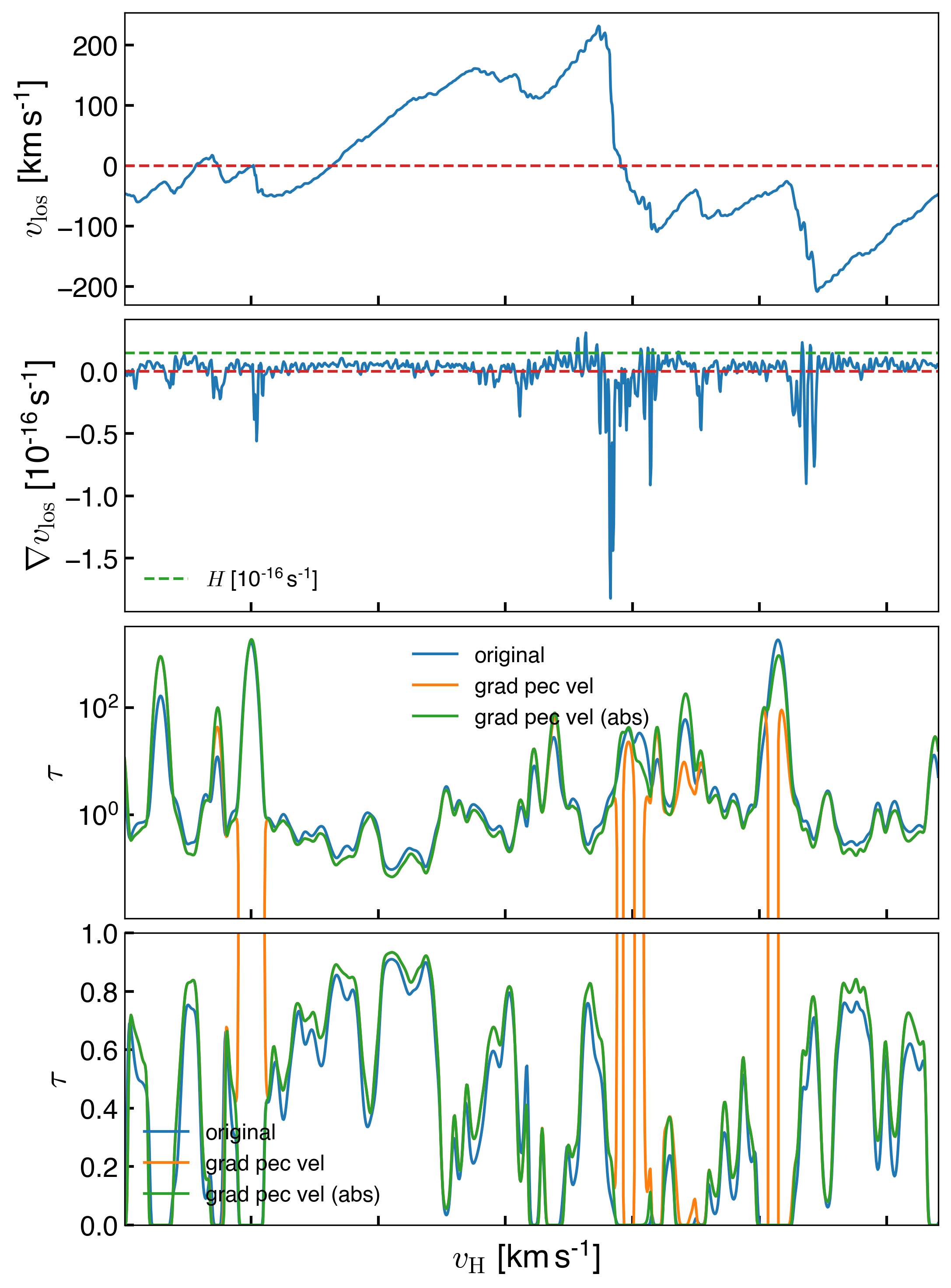
The figure below shows:
-
Peculiar velocity
-
Gradient of peculiar velocity compared to H (dashed)
-
Optical depth computed in the original way, the modified way using \(du/dr = H + \nabla v_\mathrm{pec}(r)\) and then using the absolute value $$ du/dr = H + \nabla v_\mathrm{pec}(r) $ - Transmitted flux for the three versions of \(\tau\)
Redshit = 4.2