Effects of Rescaling on the P(k)
The power spectrum is computed on the transmited flux fluctuations \(\delta_{F}\), defines as:
\[\delta_{F} \,=\, \frac{F- \overline{F} }{ \overline{F}} \,=\, \frac{F}{ \overline{F} } - 1\]Rescaling The Transmitted Flux
If we rescale the Transmitted flux along the line of sight by a factor \(\alpha\), then:
\[F^\prime = \alpha F\] \[\overline{F^\prime} = \alpha \overline{F}\] \[\delta_{F}^\prime = \delta_{F}\]Then, rescaling the Transmitted Flux has no effect on the Flux Power Spectrum
Rescaling The Optical Depth
Now, if instead we rescale the Optical Depth along the line of sight, such that:
\[\tau^\prime = \alpha \tau\] \[F^\prime = \mathrm{exp}( - \tau^\prime ) = \mathrm{exp}( - \alpha \tau ) = \mathrm{exp}( - \tau )^{\alpha}\] \[\overline{F^\prime} = \frac{1}{N} \sum \mathrm{exp}( - \tau )^{\alpha}\]where \(N\) is the number of pixels in the skewer.
Then the Flux Fluctuations become:
\[\delta_{F}^\prime = \frac{ \mathrm{exp}( - \tau )^{\alpha} }{ \frac{1}{N} \sum \mathrm{exp}( - \tau )^{\alpha} } - 1\]and the Flux fluctuations from the original optical depth:
\[\delta_{F} = \frac{ \mathrm{exp}( - \tau ) }{ \frac{1}{N} \sum \mathrm{exp}( - \tau ) } - 1\]seems like the Flux fluctuations from the rescaled optical depth \(\delta_F^{\prime}\) can not be expressed as linear transformation from the original \(\delta_F\), which would result in an scale dependent rescaling of the Flux Power Spectrum.
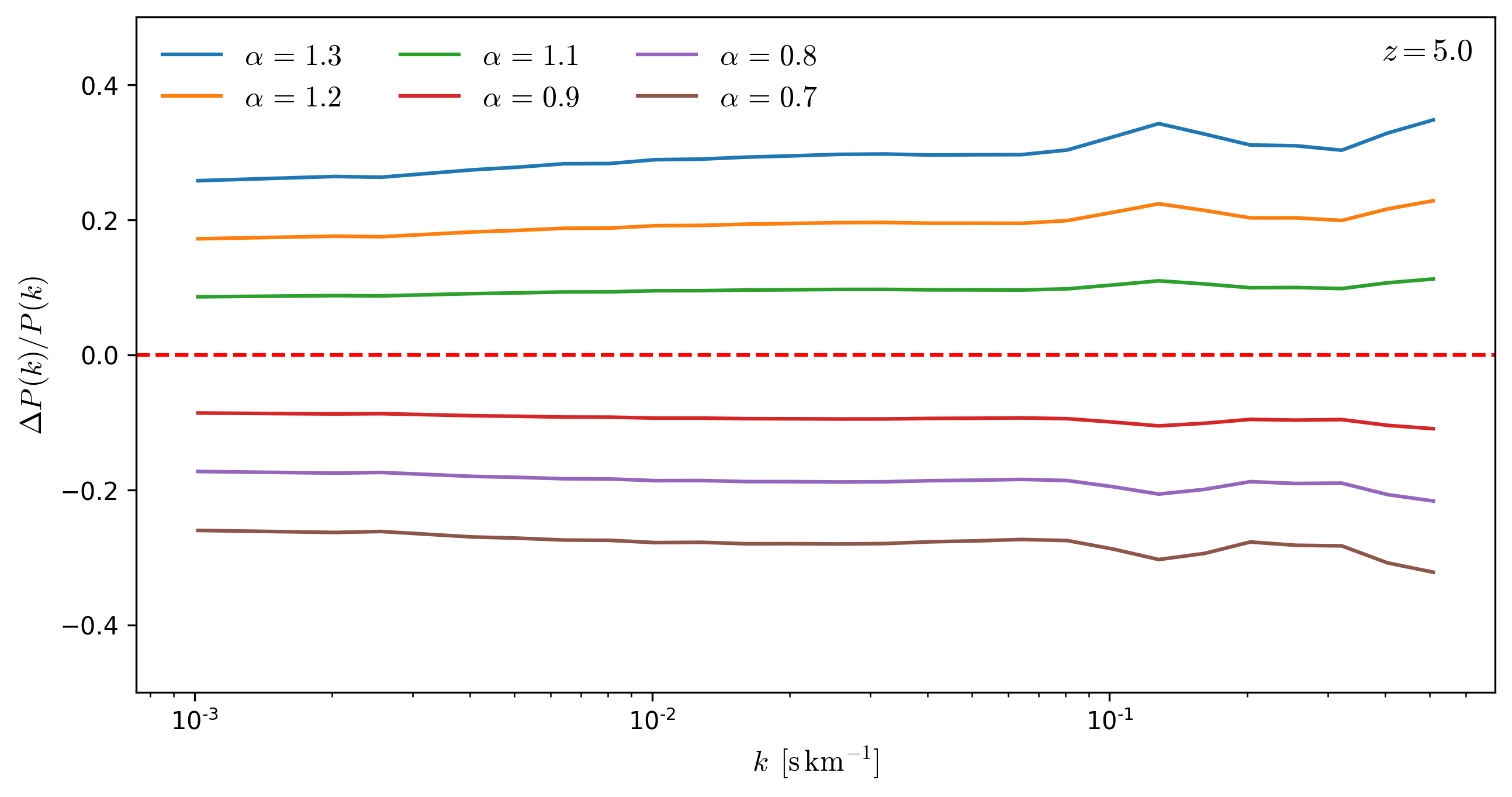
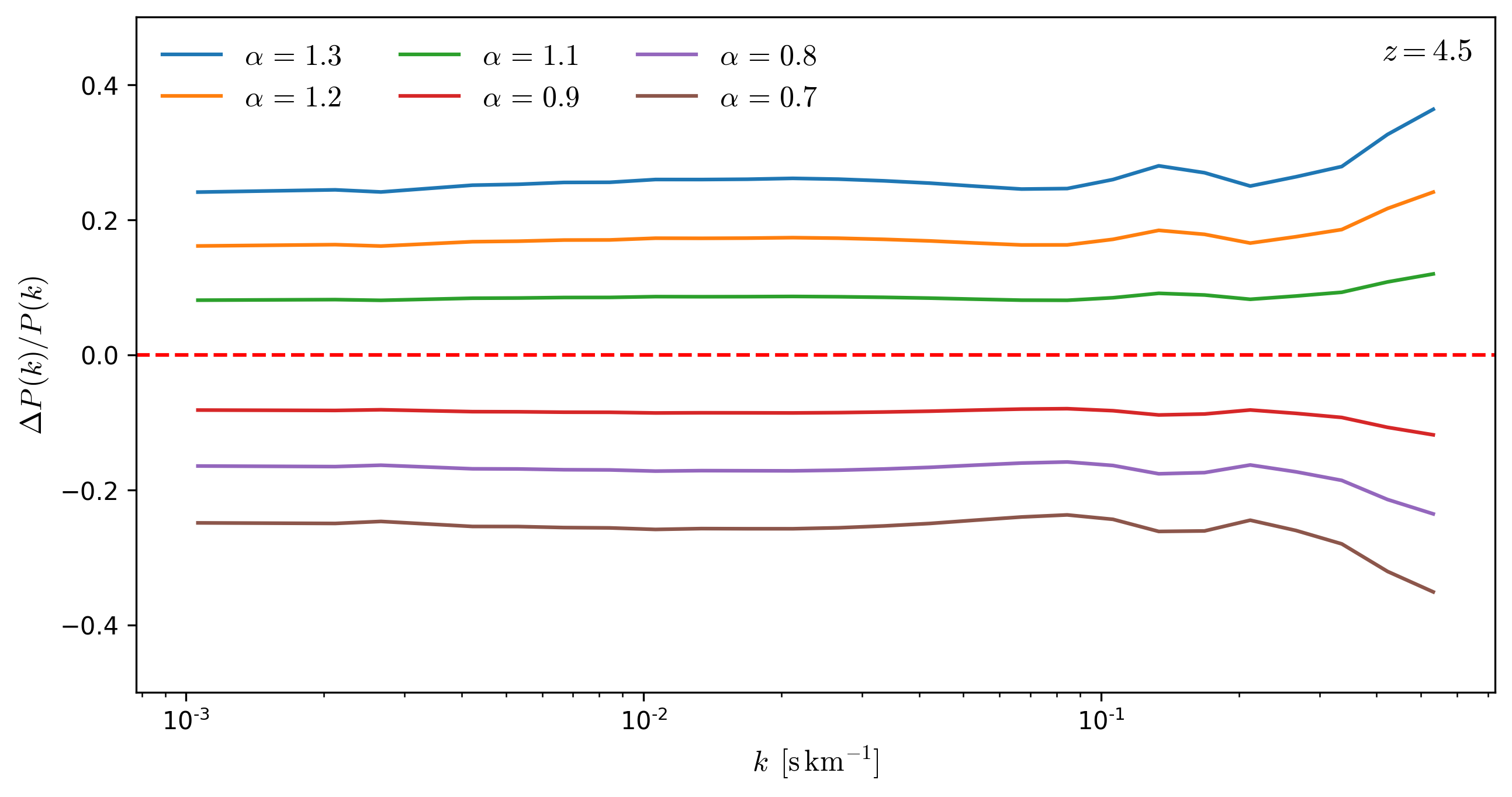
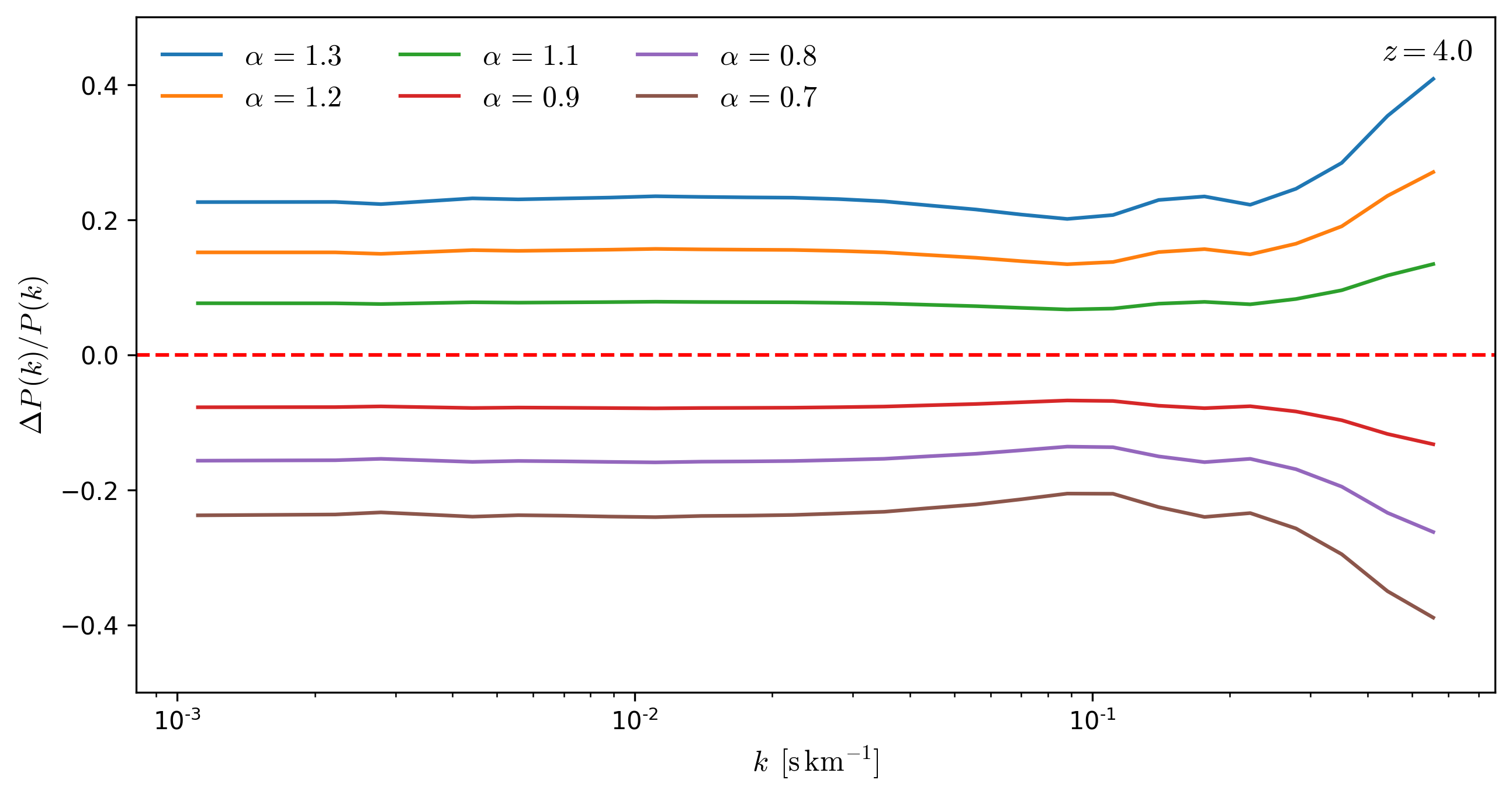
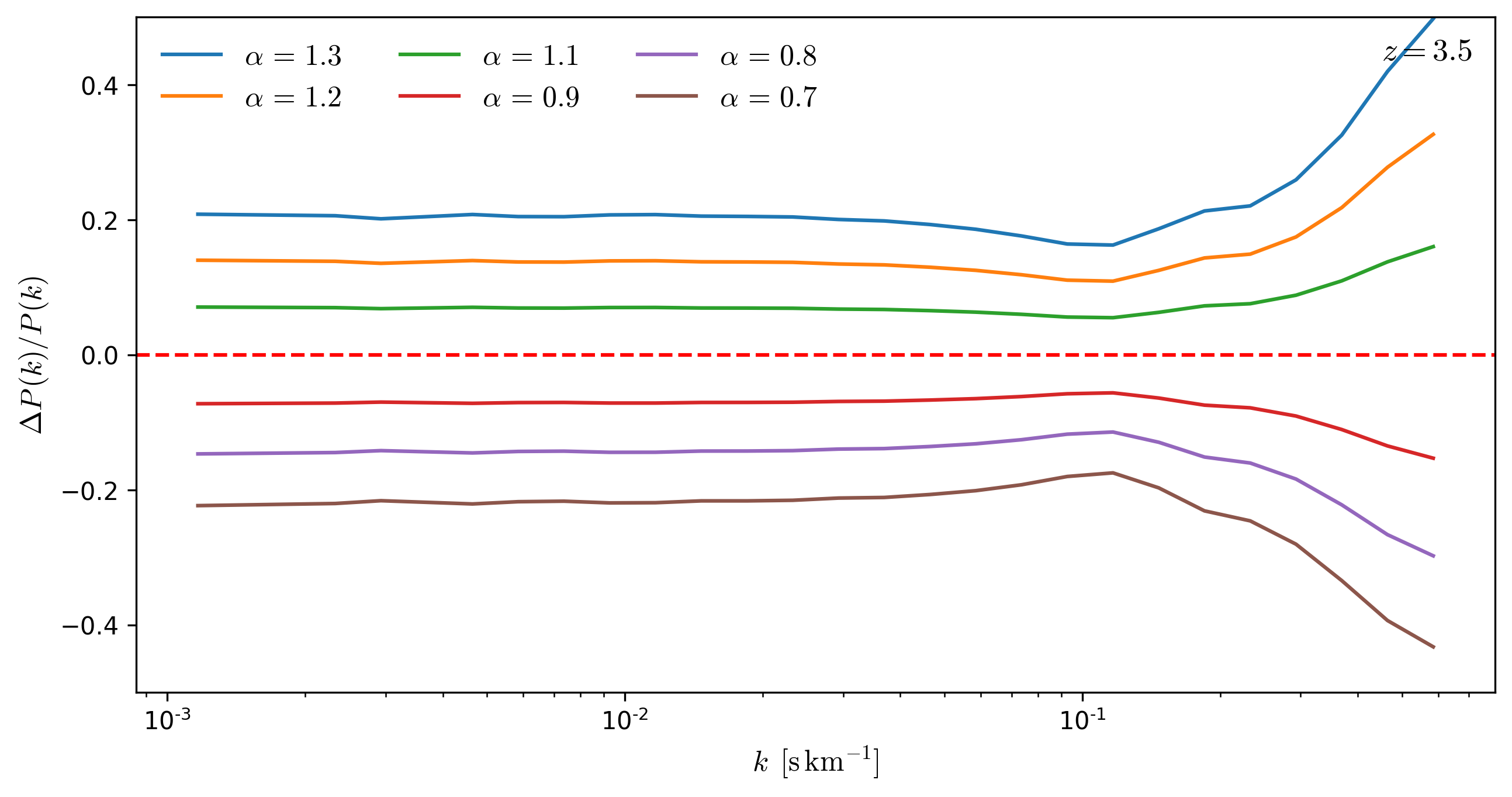
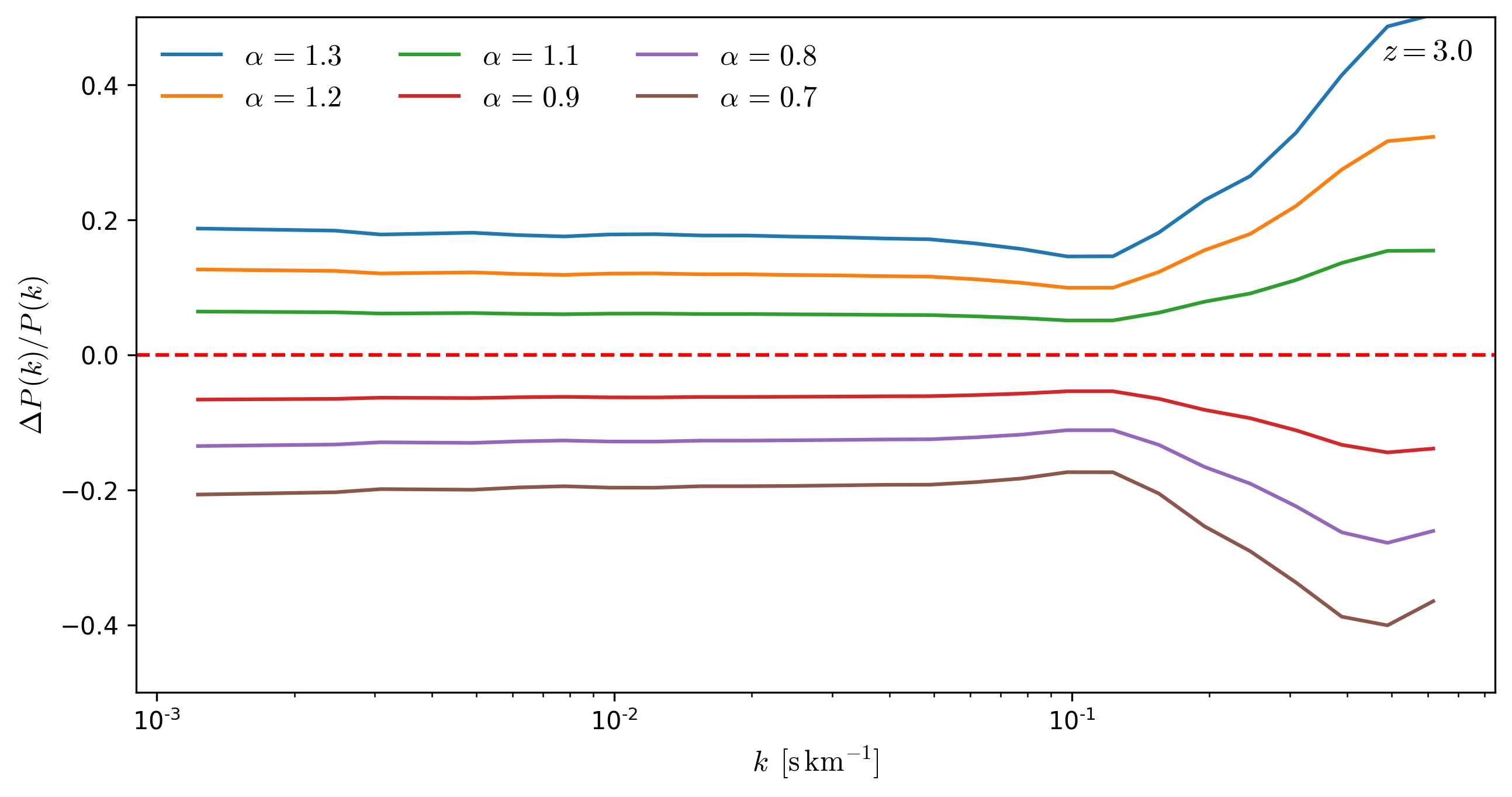
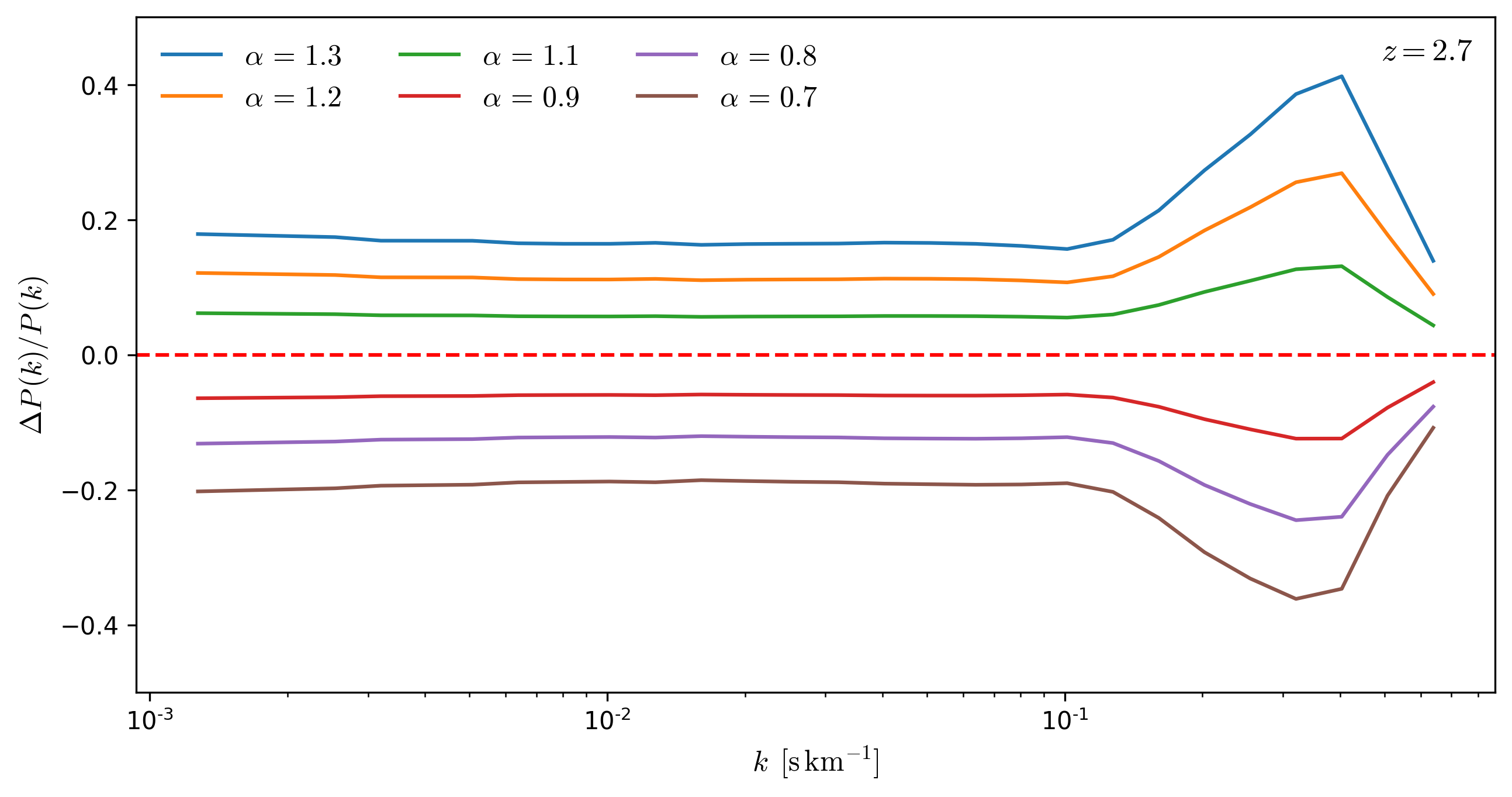
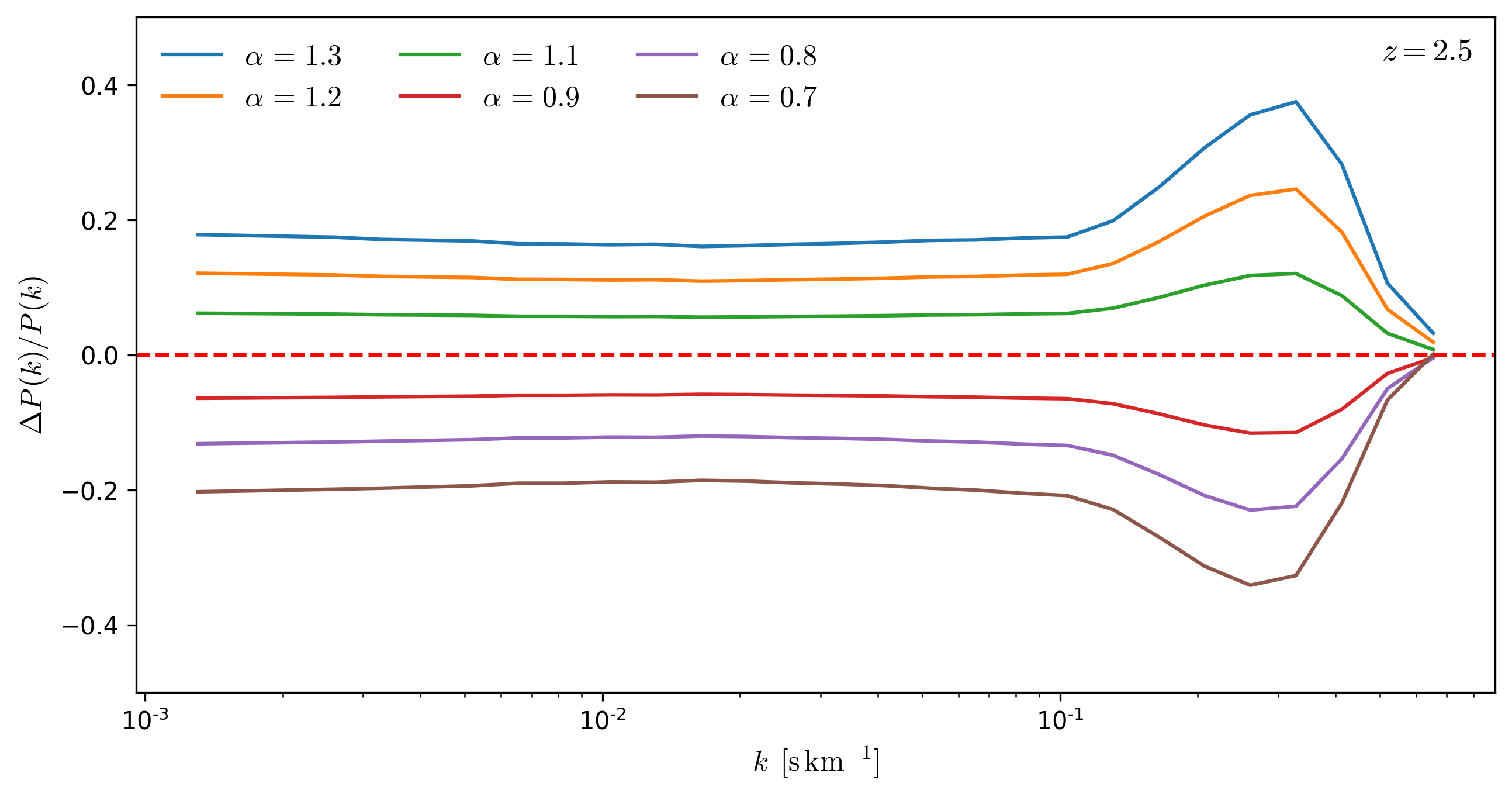
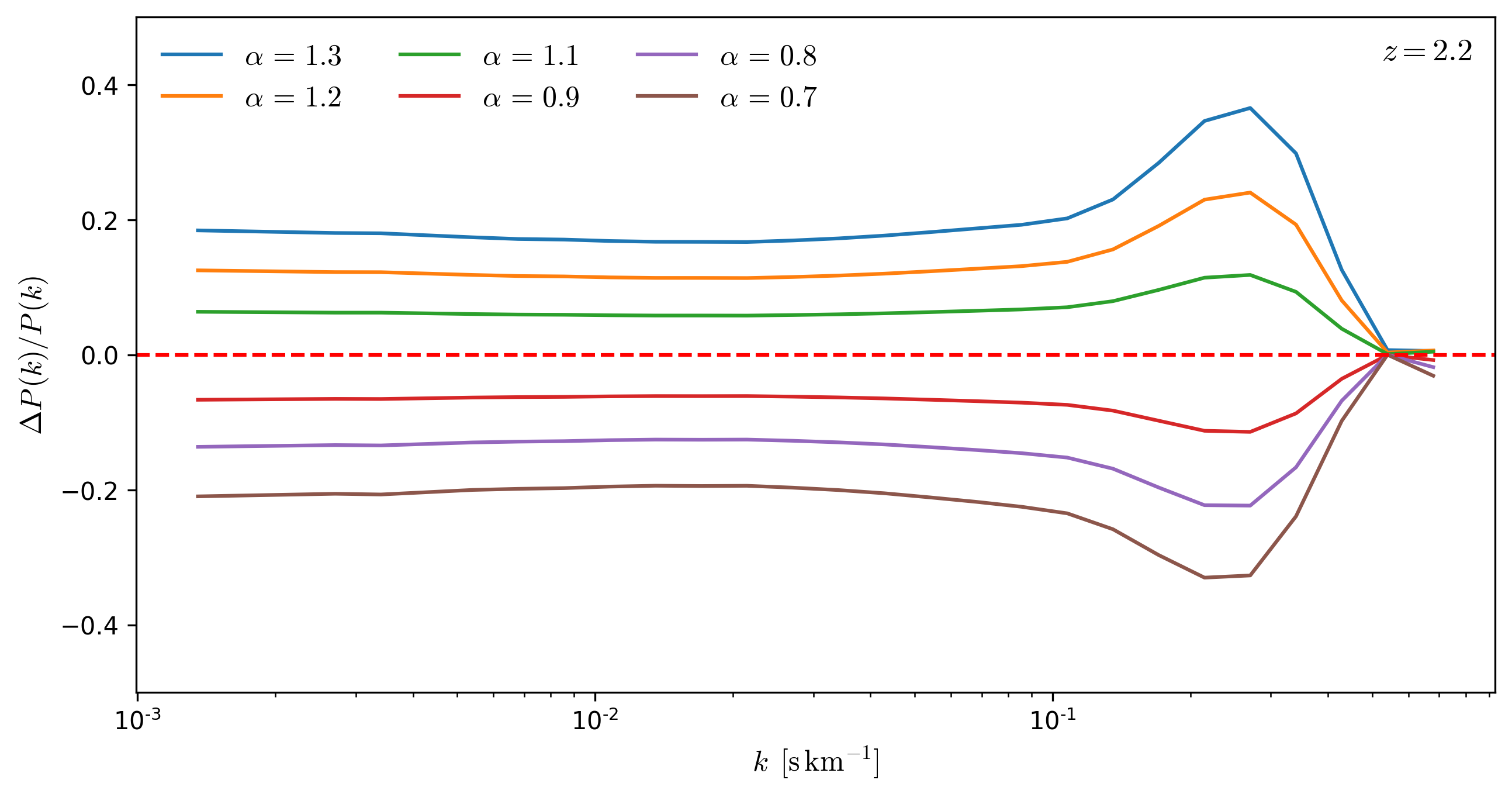
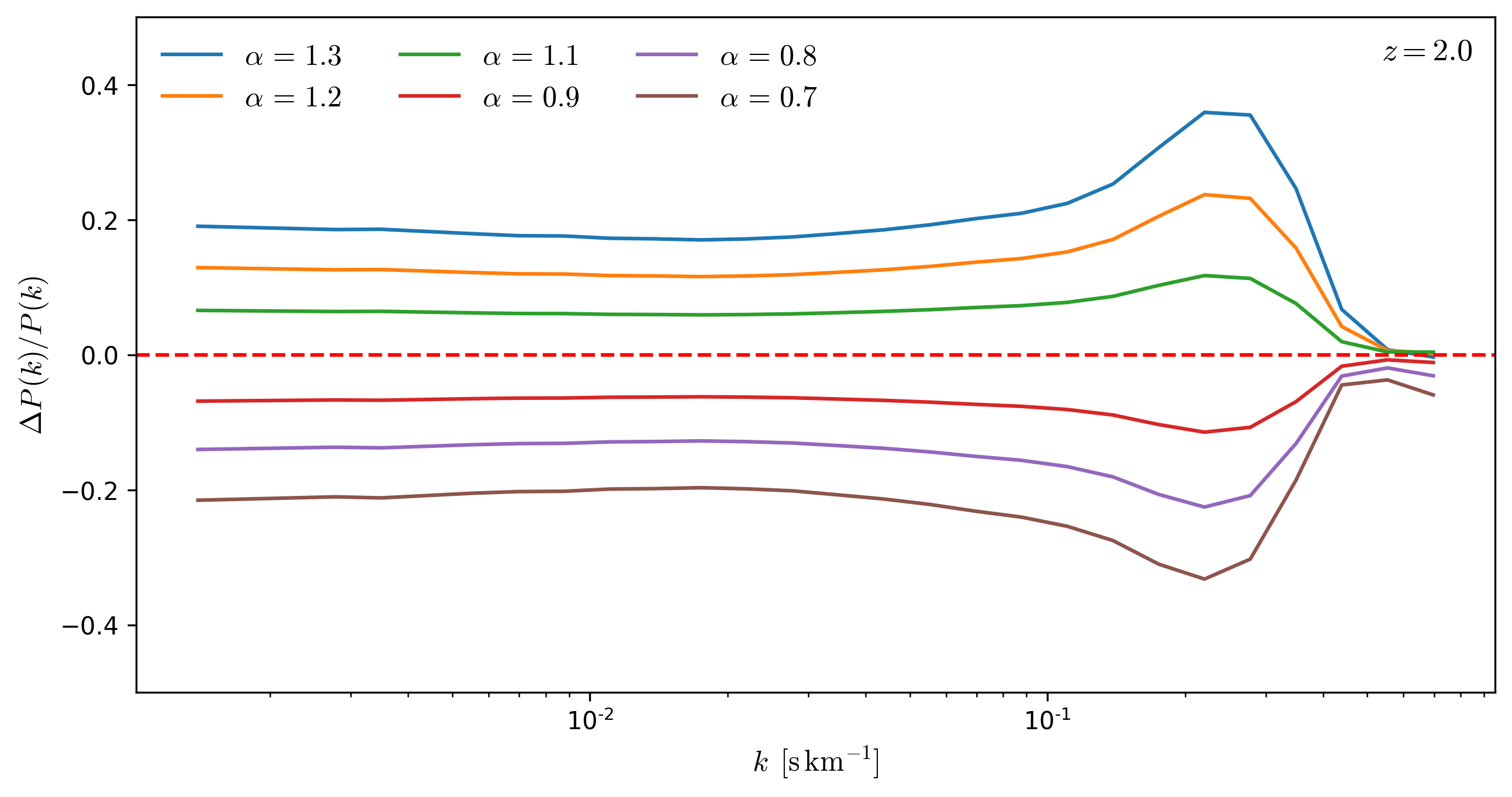
Effects rescaling \(\tau\) as a function of redshift
To evaluate the effect that rescaling \(tau\) has on the Flux Power Spectrum, I rescale \(tau\) from the skewers in a snapshot by a factor \(\alpha\) and compare the resulting \(P(k)\) to the original \(P(k)\), the results for several redshifts are shown below.
From the figures below, it can be seen that **the effects of the rescaling \(\tau\) on \(P(k)\) are mostly scale independent for \(k < 0.1\). **