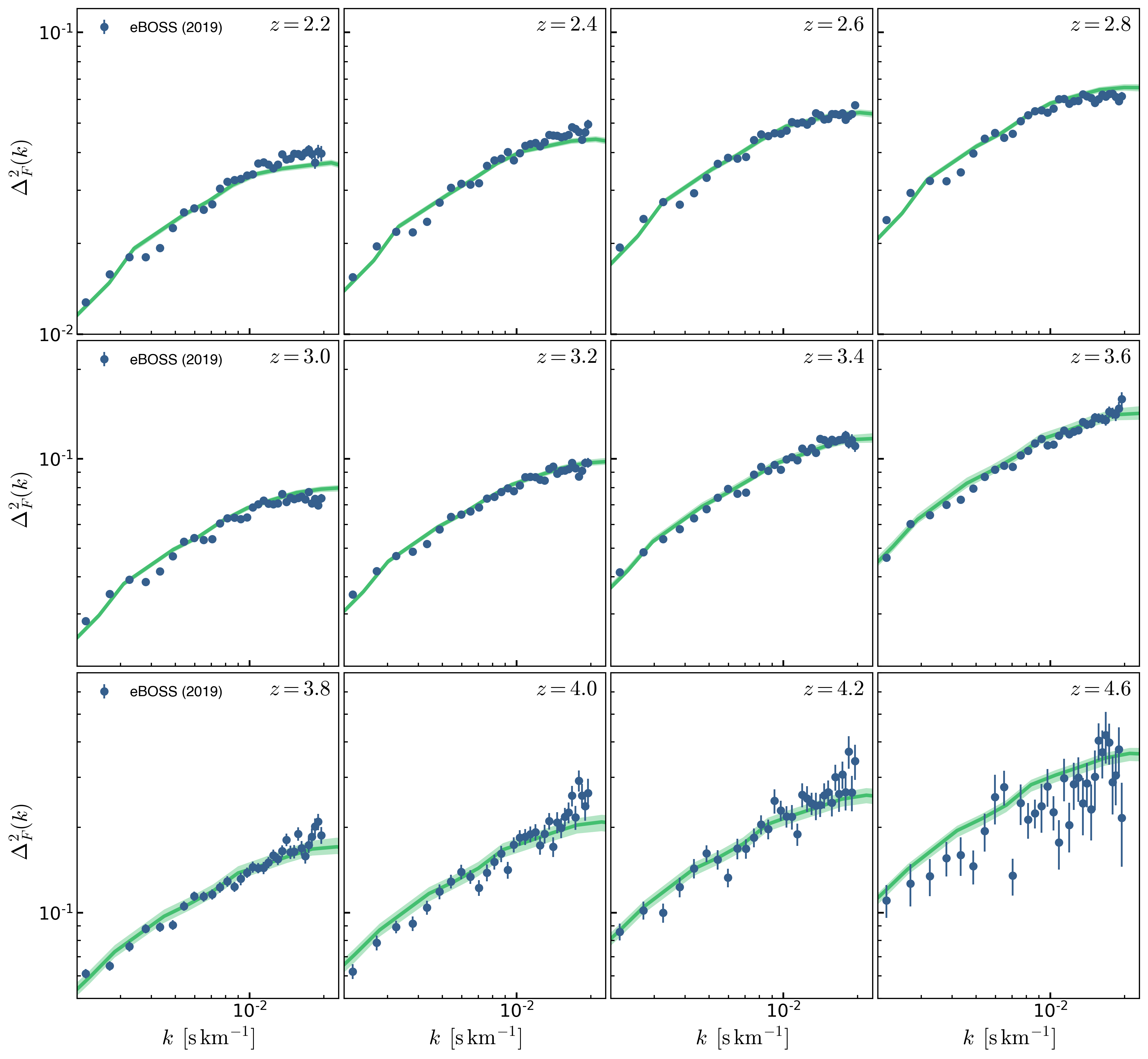
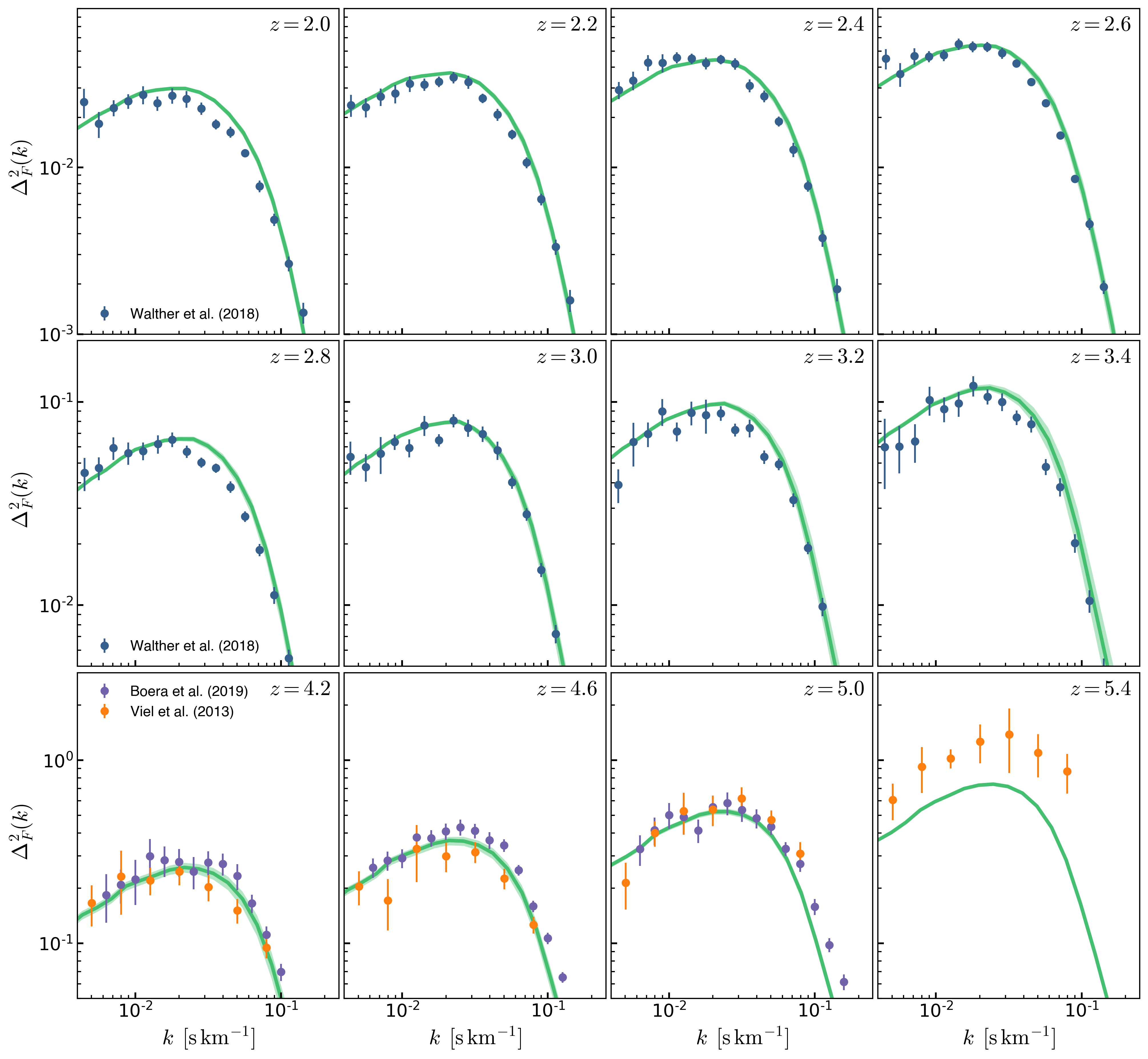
P(k) Sampling
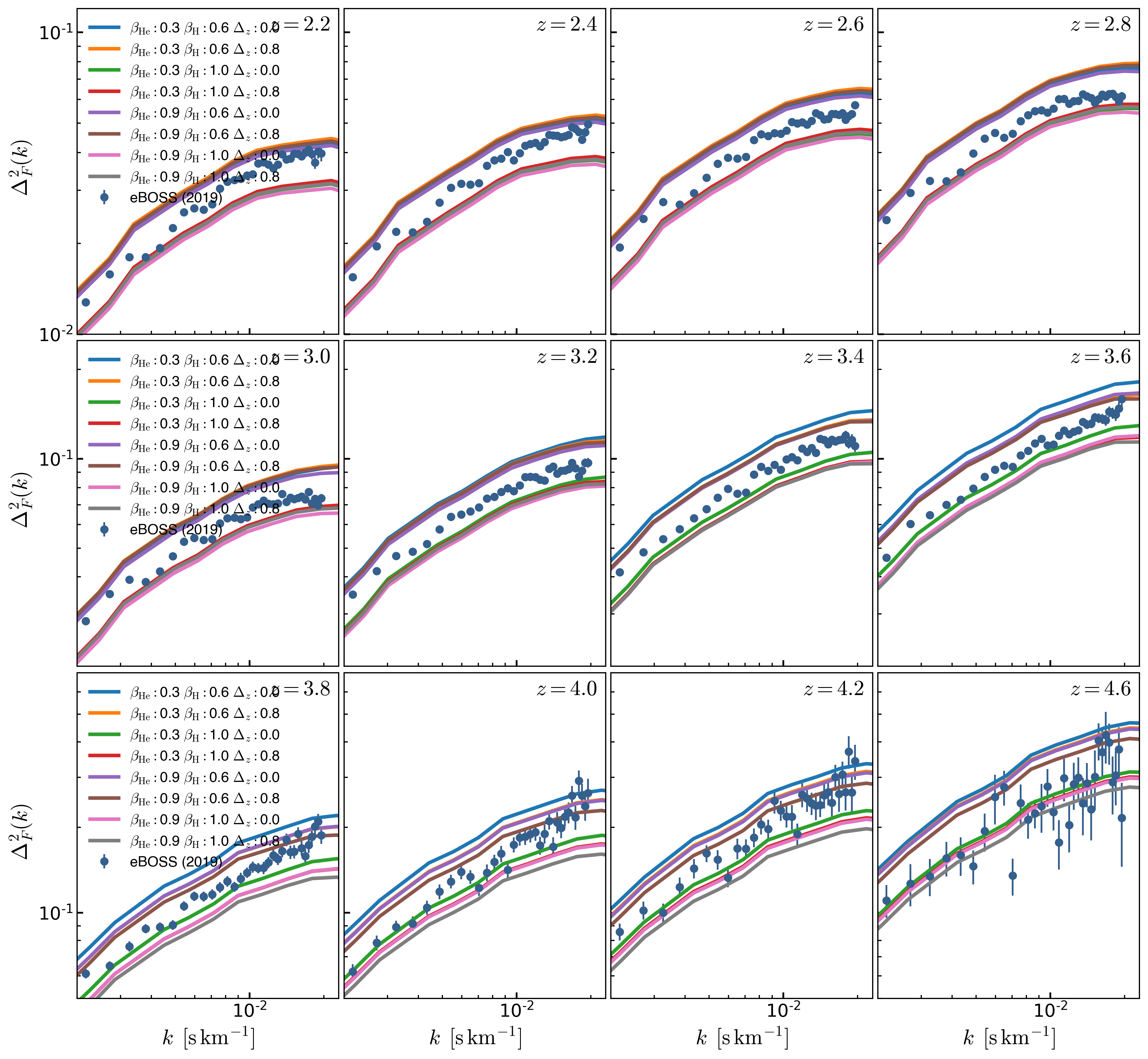
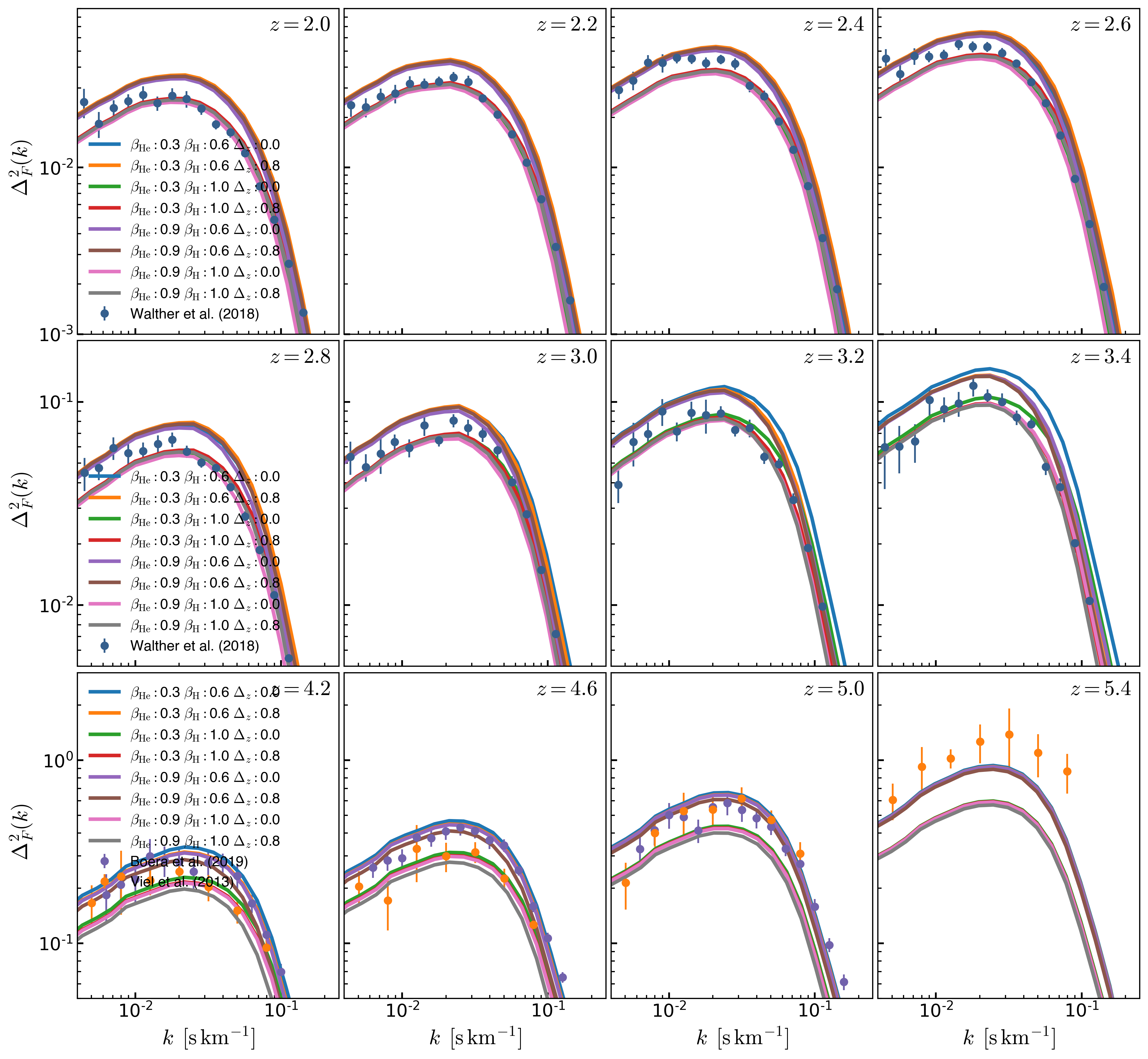
From a set of 8 \(1024^3\) simulations where the parameters are:
\(\beta_{\mathrm{He}} = [0.3 \,\,\,\, 0.9 ]\) \(\beta_{\mathrm{H}} = [0.6 \,\,\,\, 1.0 ]\) \(\Delta z_{\mathrm{He}} = [0.0 \,\,\,\, 0.8 ]\)
The mean \(P(k)\) from each simulation is shown below, as expected changing \(\beta_{\mathrm{H}}\) results in the largest change in P(k) as the normalization changes:
The 95% highest probability interval of P(k) resulting from uniformly sampling the parameters is show below:
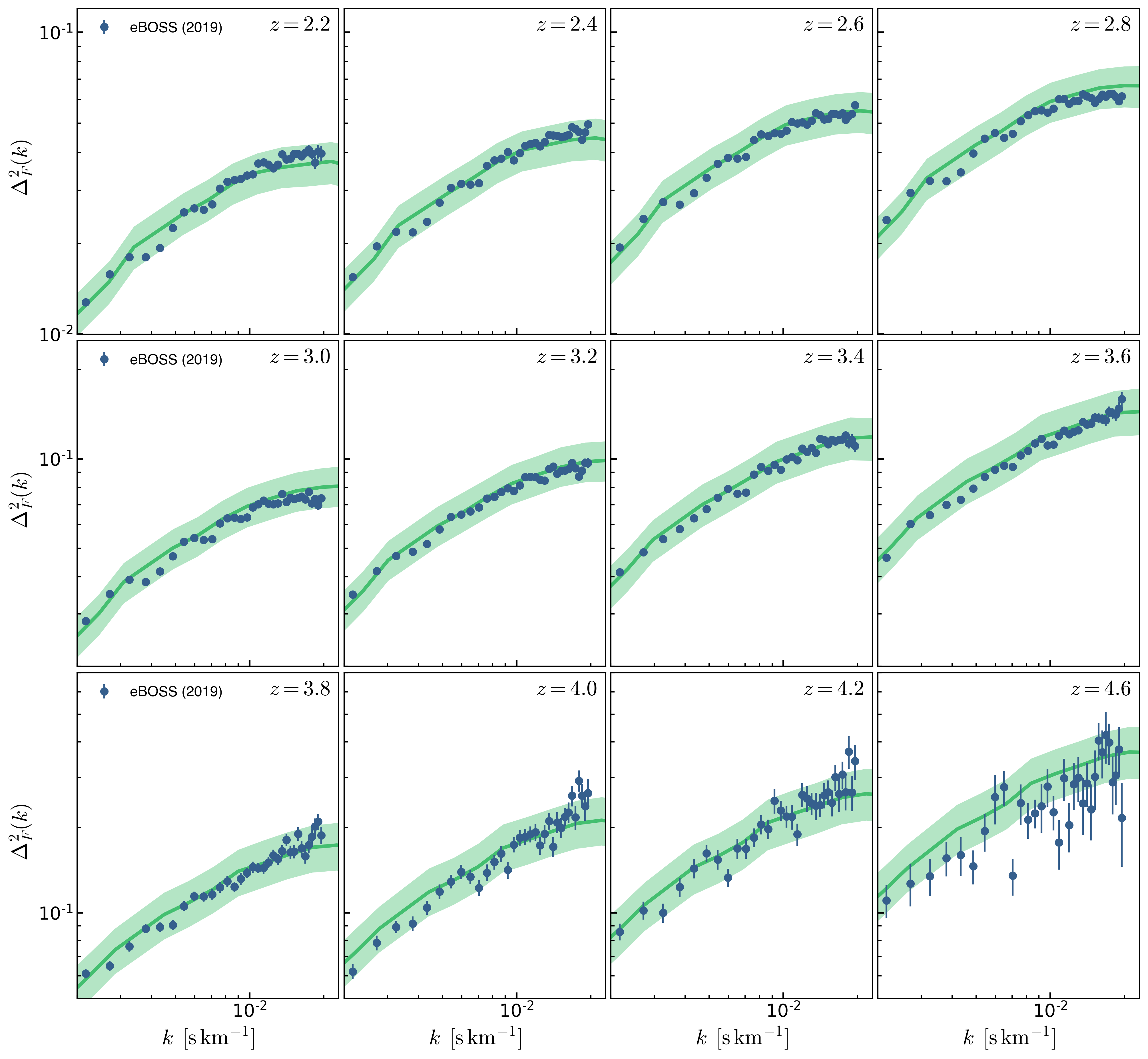
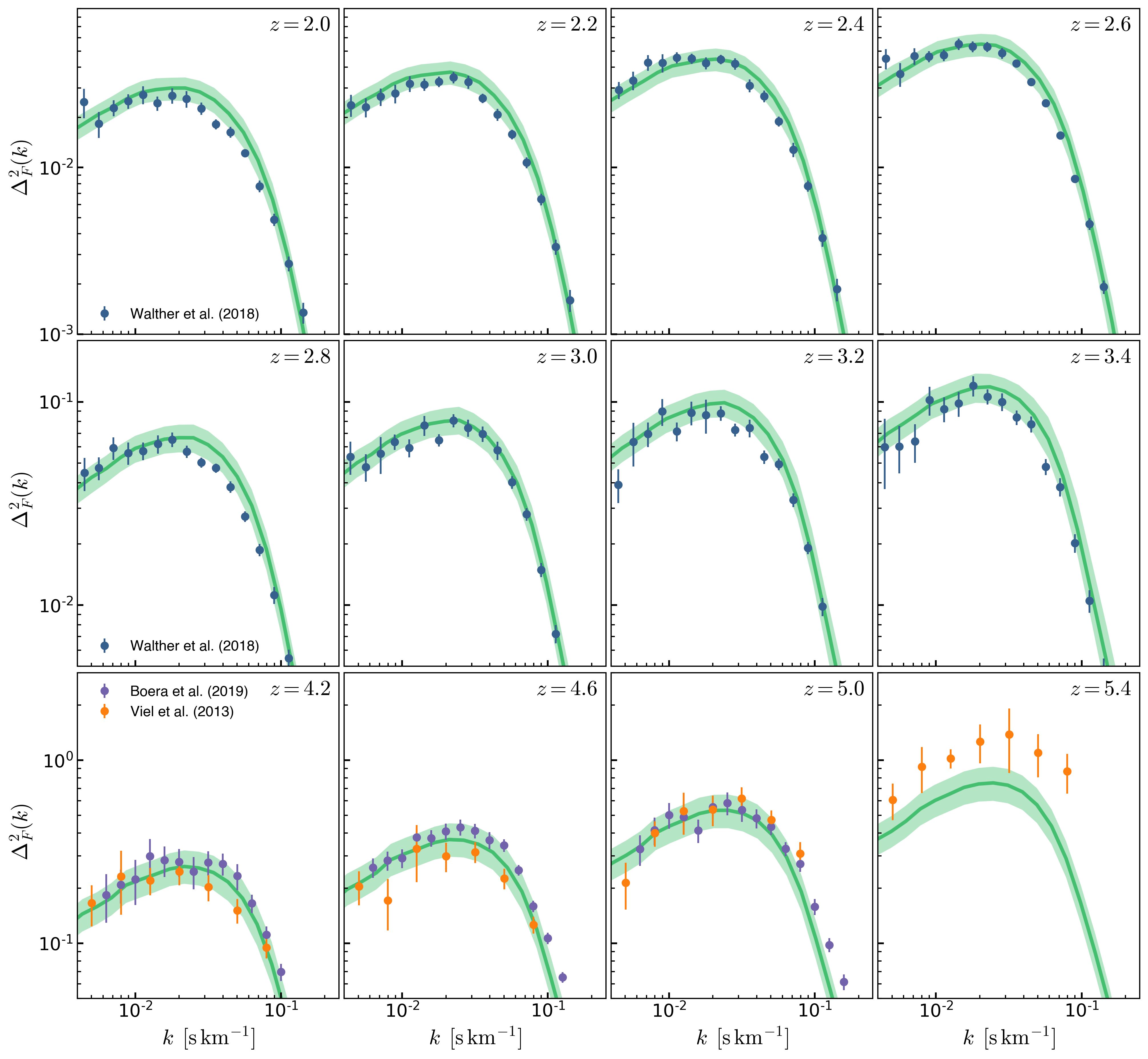
To quantify the effects of varying \(\beta_{\mathrm{He}}\) and \(\Delta z_{\mathrm{He}}\), I fixed \(\beta_{\mathrm{H}}=0.8\) ans sample P(k) uniformly changing \(\beta_{\mathrm{He}}\) and \(\Delta z_{\mathrm{He}}\) only, below is the 95% highest probability interval of P(k):