P(k) MCMC Fit to Boss Data

From a set of 8 $1024^3$ simulations where the parameters are:

$\beta_{\mathrm{He}} = [0.3 \,\,\,\, 0.9 ]$ $\beta_{\mathrm{H}} = [0.6 \,\,\,\, 1.0 ]$ $\Delta z_{\mathrm{He}} = [0.0 \,\,\,\, 0.8 ]$

First I fit each redshift independently:

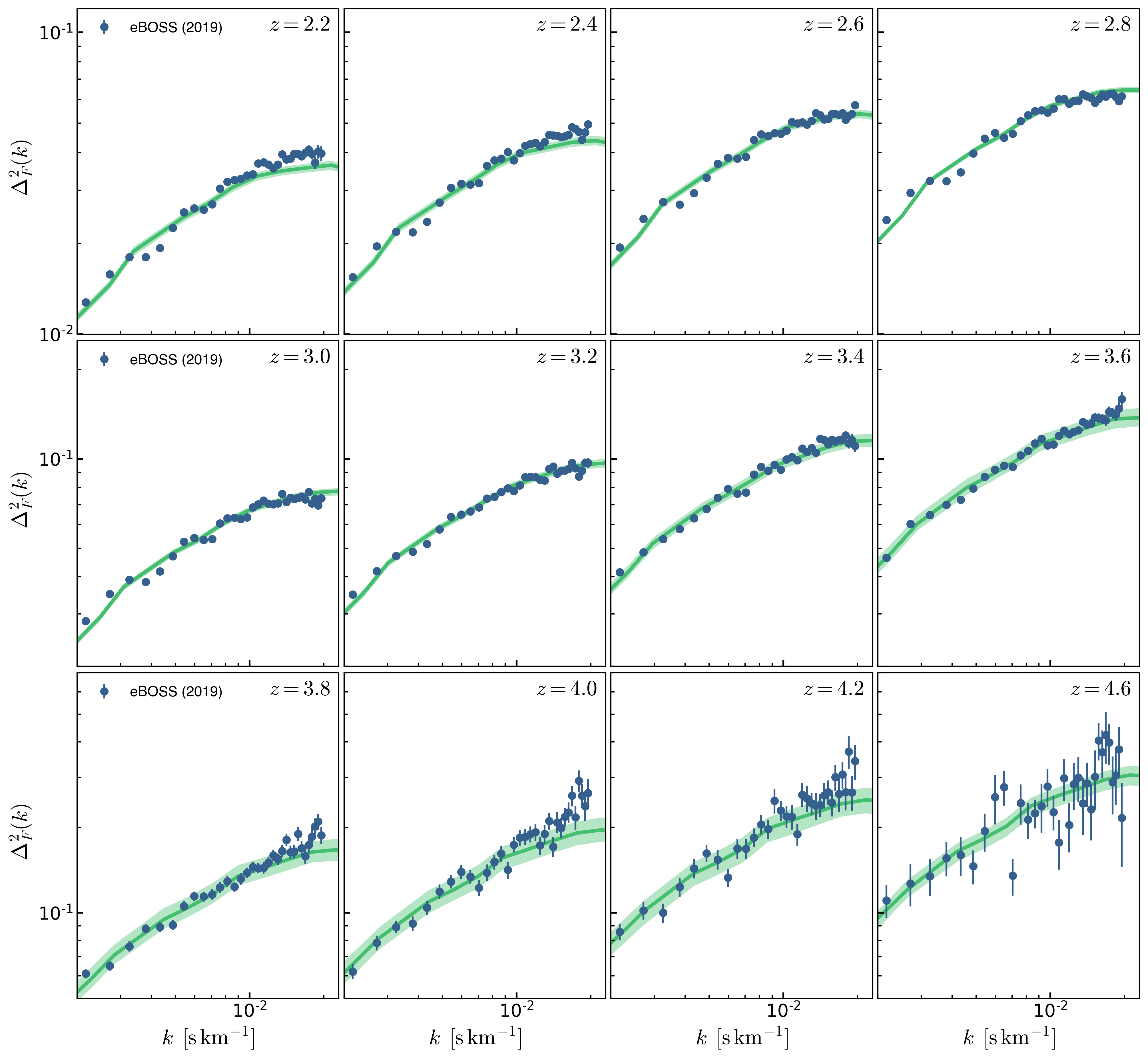
The 95% Highest Probability Interval from the posterior distribution of the fitted parameters ( as a function of redshift, since each redshift is fitted independently ) is shown below, there are no constrains for the Helium parameters:

Now I fit all the redshifts simultaneously:

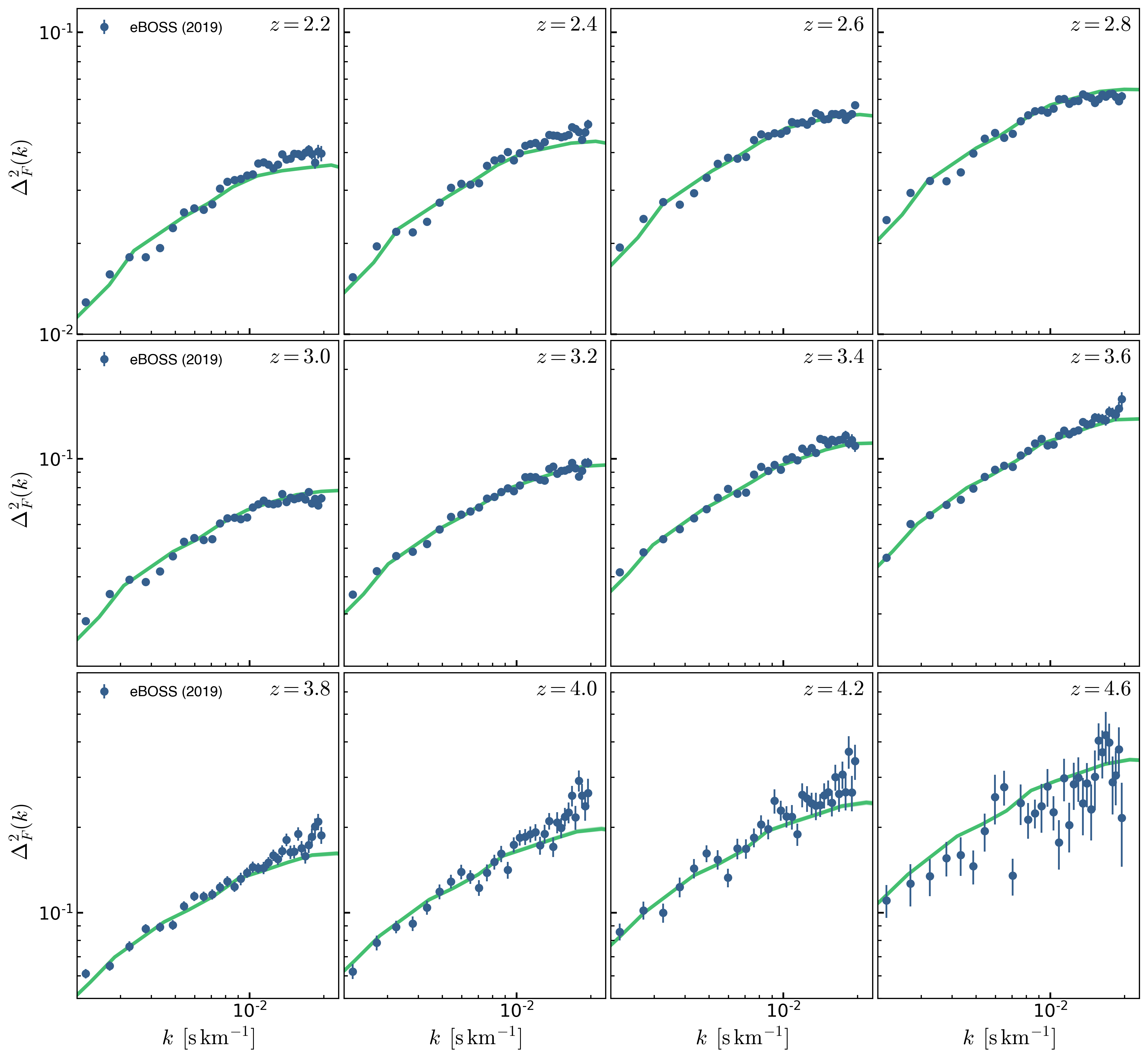
And the posterior distribution of the parameters are:

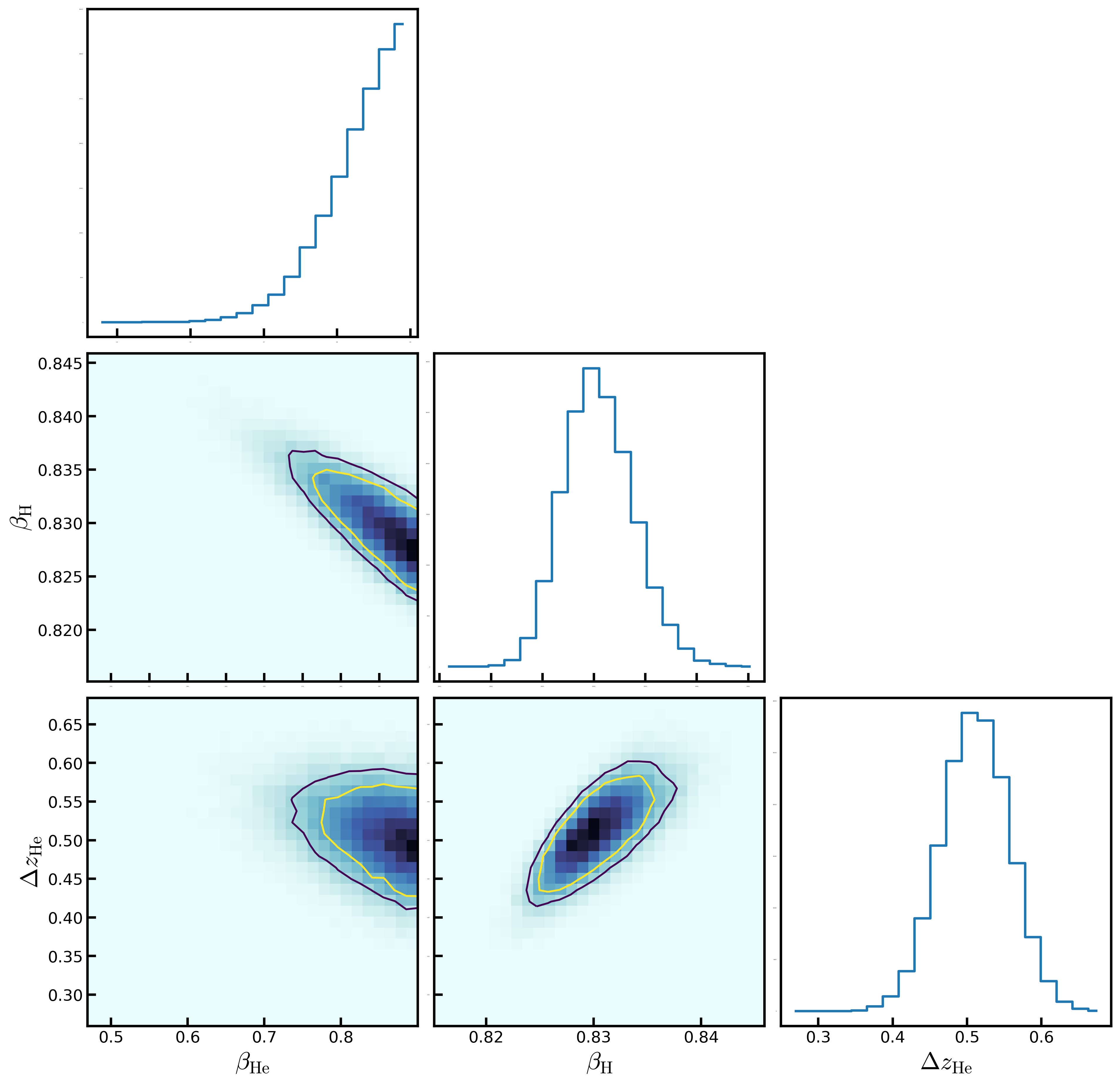
Resulting in a delayed Helium reionization but with High photoheating and photoinization rates.