Sheth & Tormen 1999

From the Sheth & Tormen 1999 halo mass function I compute the number of halos in a 50 \(h^{-1}\)Mpc box:

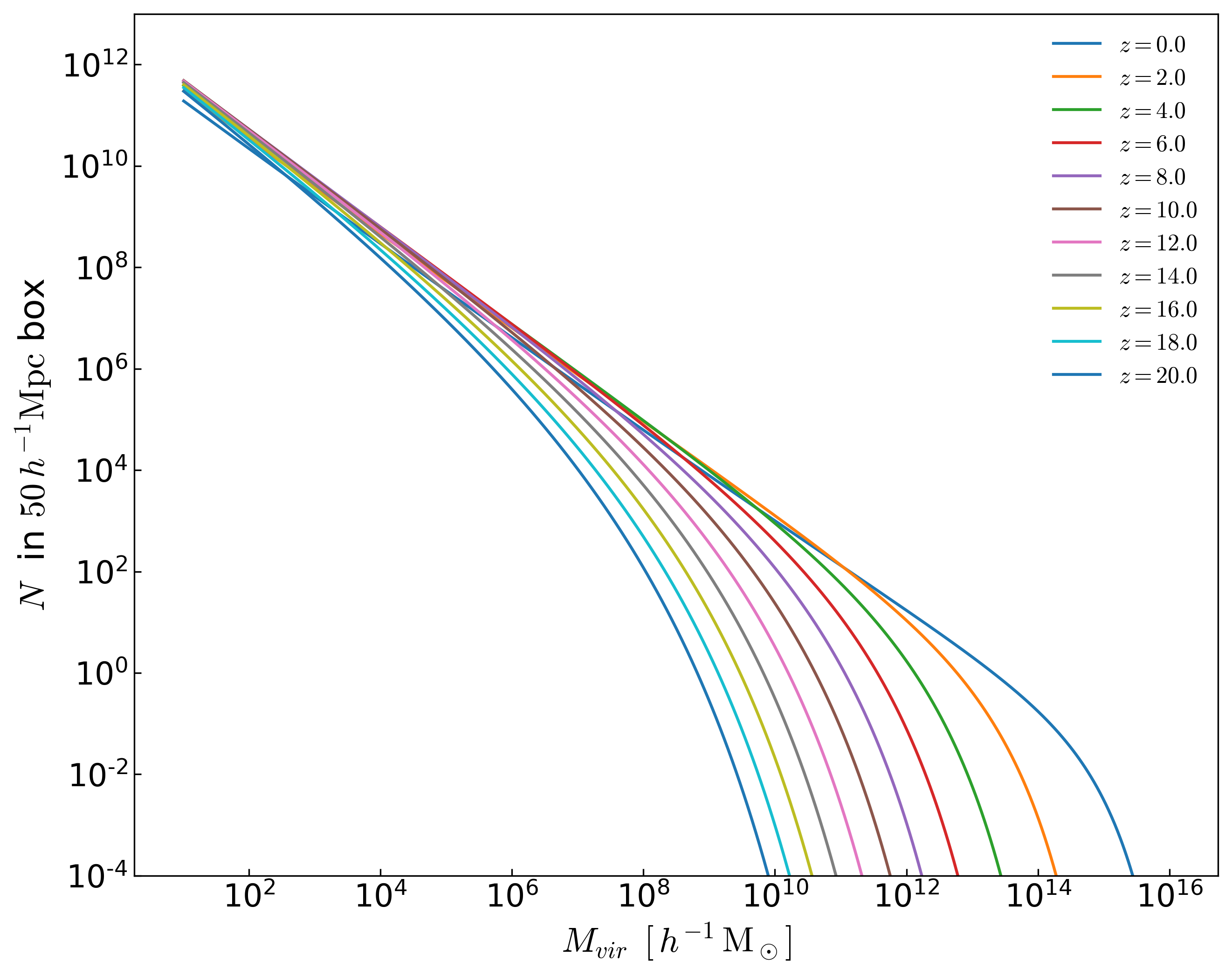
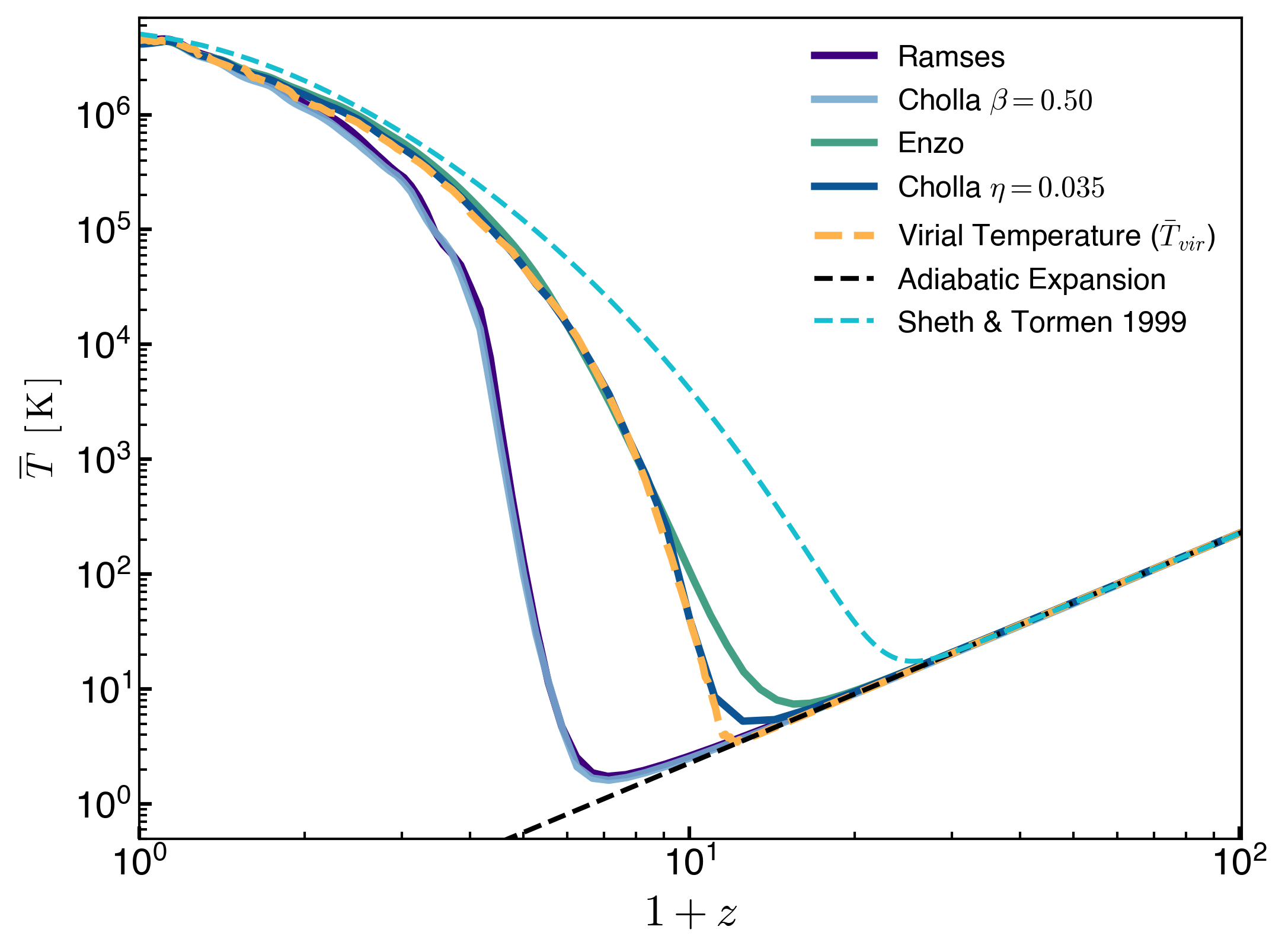
From the analytical number of halos obtained from the mass function, I compute the mean virial temperature and compare to the simulation measurements:

The Halo M_vir range used for this calculation is \(10\) Msun/h to \(10^{18}\) Msun/h:

Now if I limit the minimum halo mass in the calculation to \(M_{min}= 6.4 \times 10^{10} \, h^{-1}\mathrm{M_\odot}\), which correspond to 100*particle_mass, and what we define as the cut for resolved halos, now the analytical temperature looks much more like the temperature from the simulations:

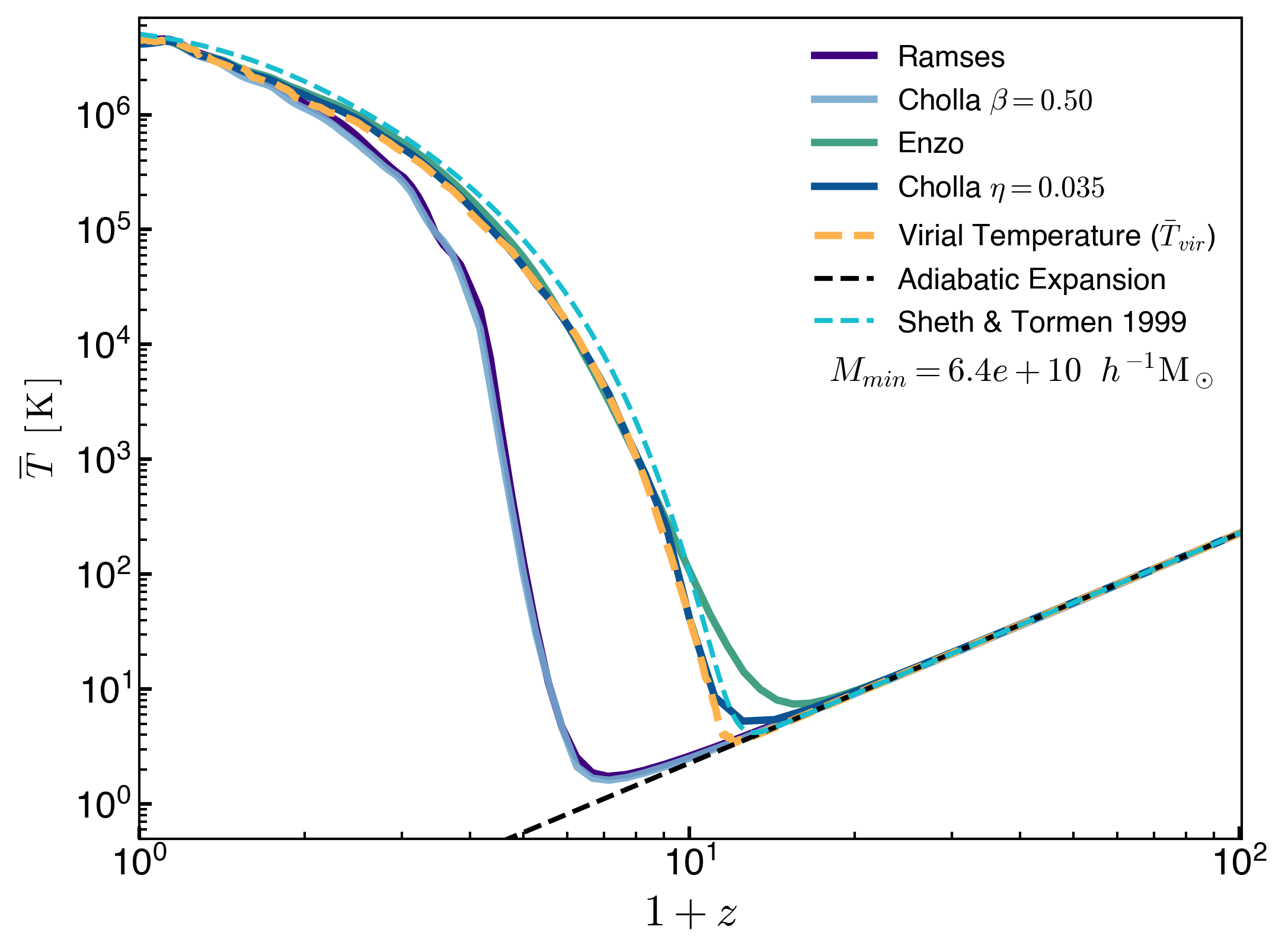
This proves that the missing unresolved small halos are responsible for the “sharp corner” in our temperature estimate from the simulations.

Press & Schechter

From the Press & Schechter formalism I compute the number of halos in a 50 \(h^{-1}\)Mpc box:

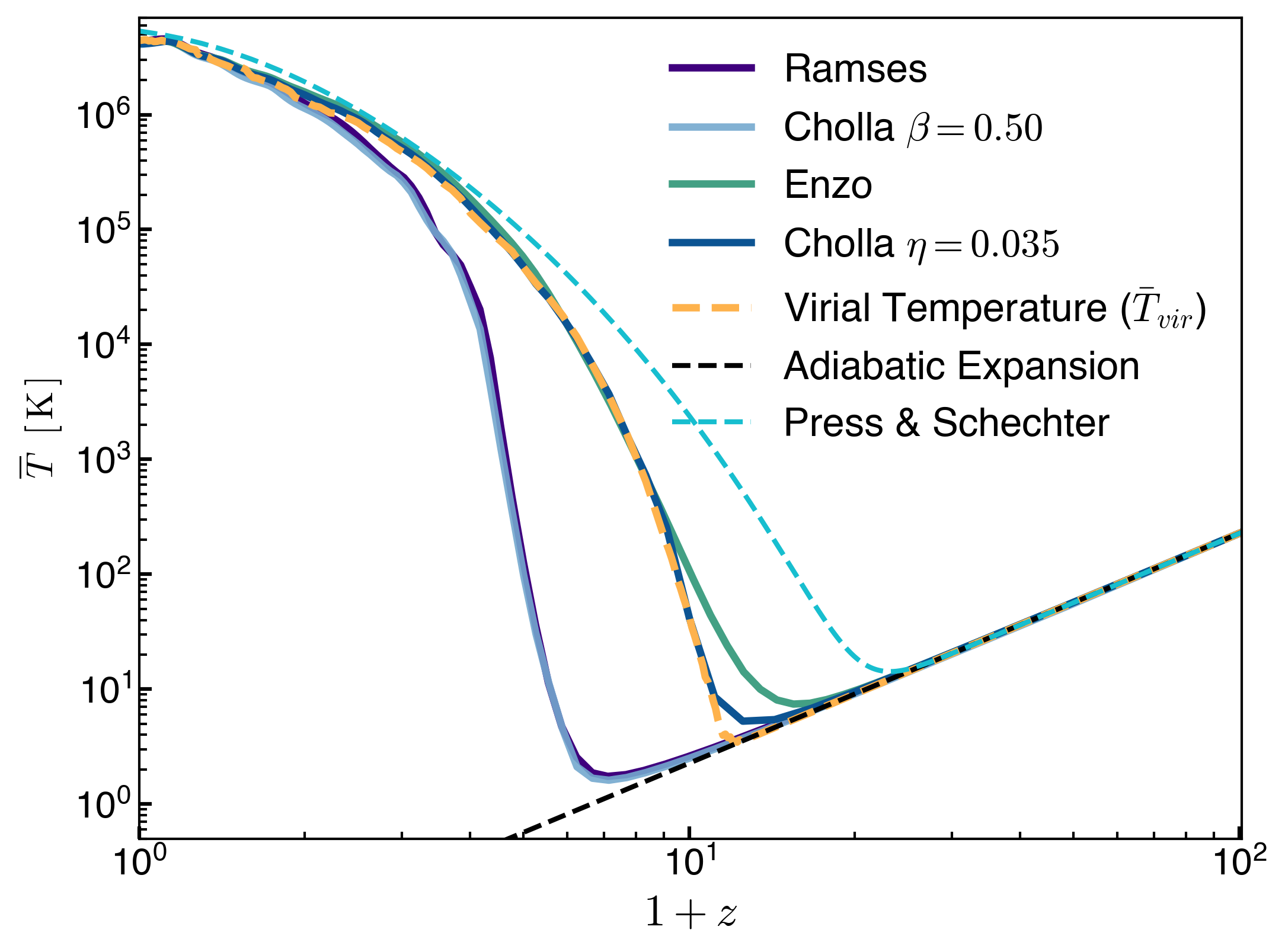
From the analytical number of halos I compute the mean virial temperature and compare to the simulation measurements:

The Halo M_vir range used for this calculation is \(10\) Msun/h to \(10^{18}\) Msun/h: