Bootstrap P(k)
From a total of \(N_{T}=60000\) skewers randomly chosen from the simulations I bootstrap the mean \(P(k)\) by selecting samples of \(N_s\) skewers and computing the mean from each sample, this is iterated 10000 times and from the obtained distribution of \(\overline{P(k)}\) the covariance matrix is computed.
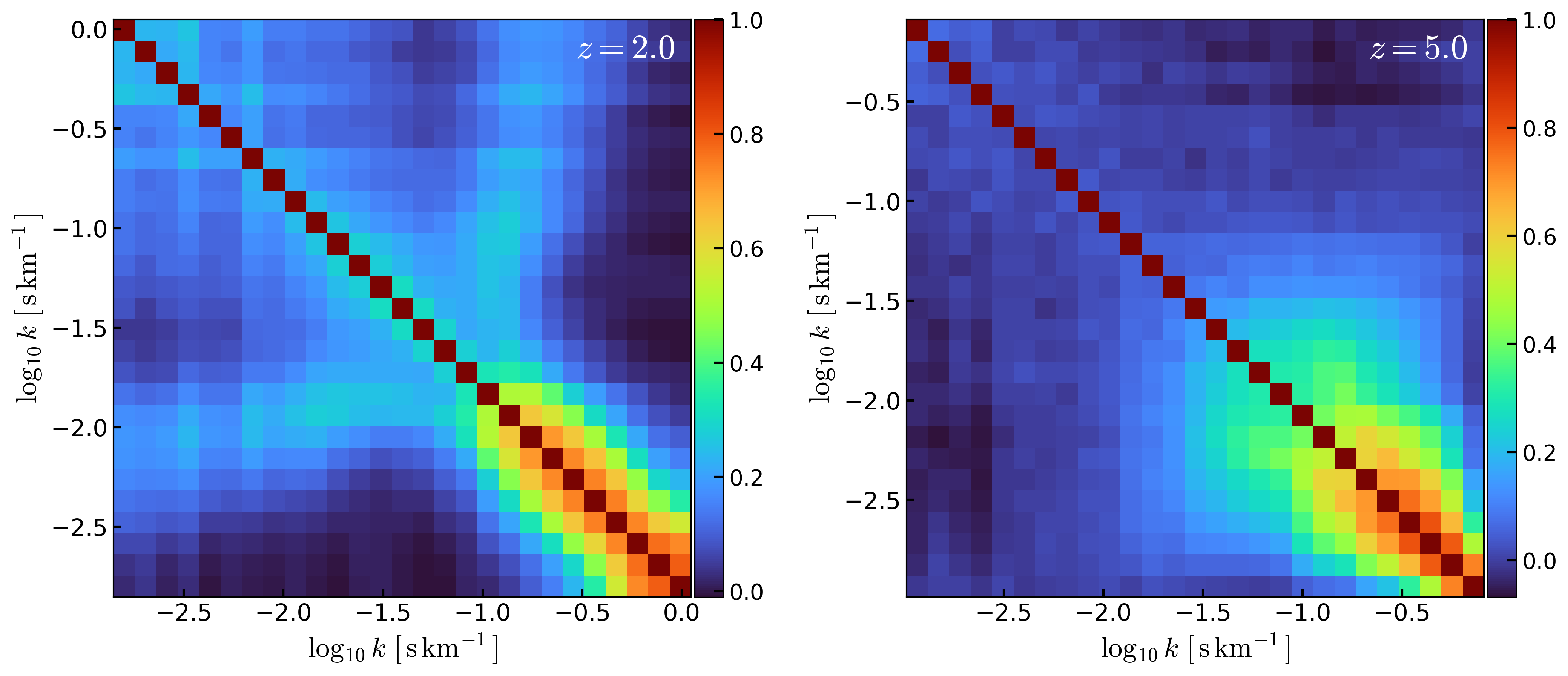
Below is the normalized ( \(C_{i,j} / \sqrt{C_{i,i} \,C_{j,j}}\) ) covariance matrix for the \(N_s=50000\) bootstrap at \(z=2\) and \(z=5\).
The standard deviation of the power spectrum is computed from the diagonal of the covariance matrix, below I show the fraction of \(\sigma\) to \(P(k)\)
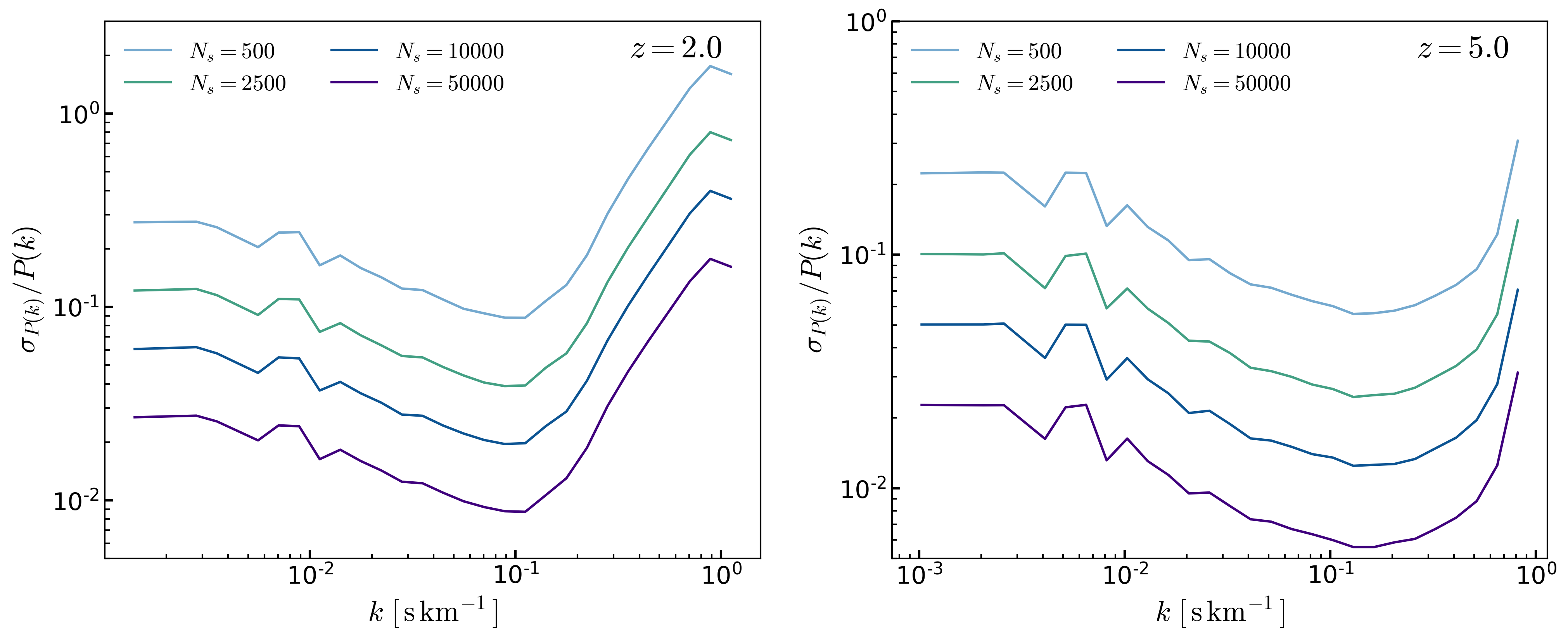
As shown, the standard deviation is proportional to \(1/\sqrt{N_s}\), if I choose the \(\sigma\) resulting from the \(N=5000\) bootstrap then \(\sigma/P(k) \sim 0.1\).
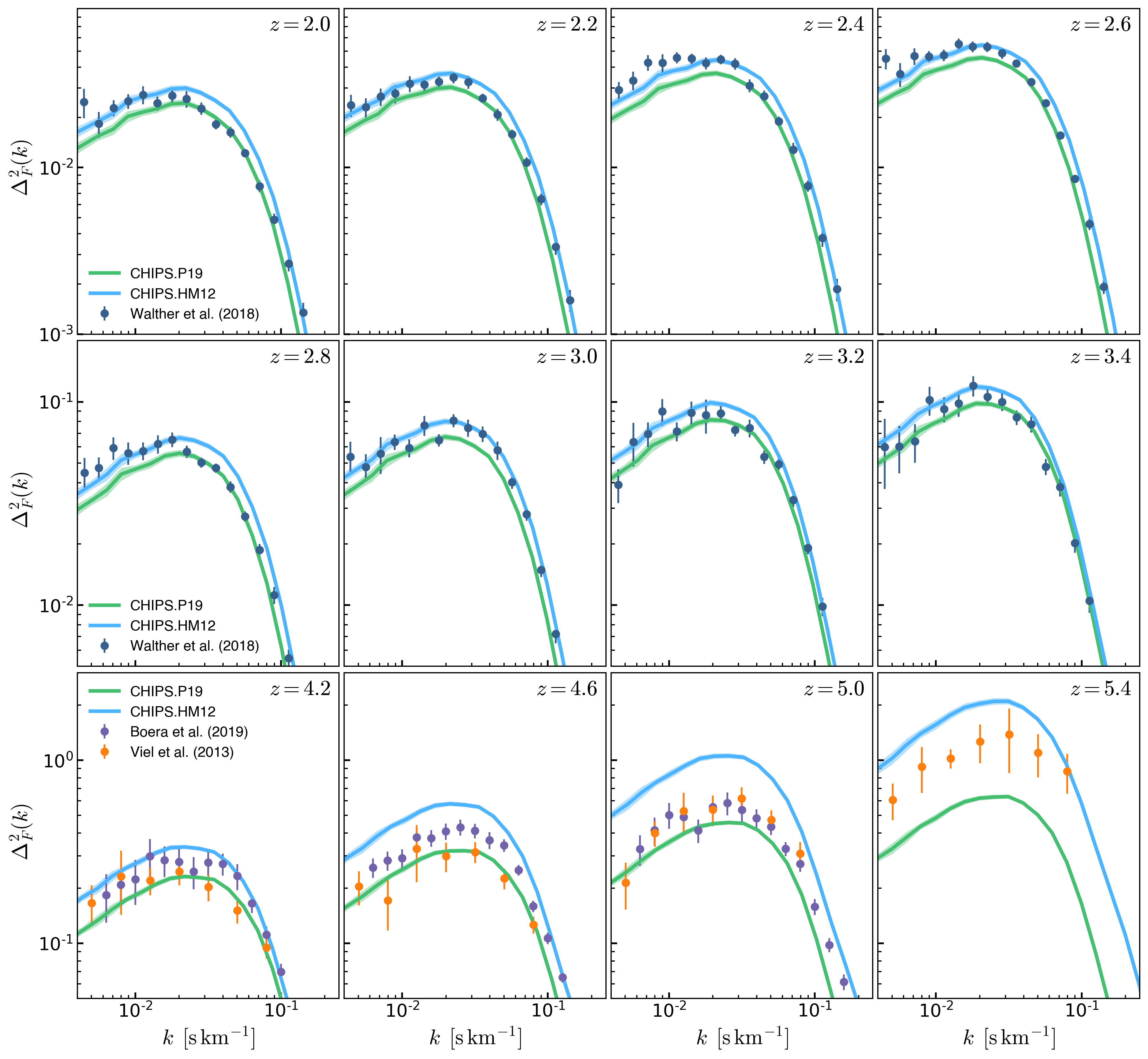
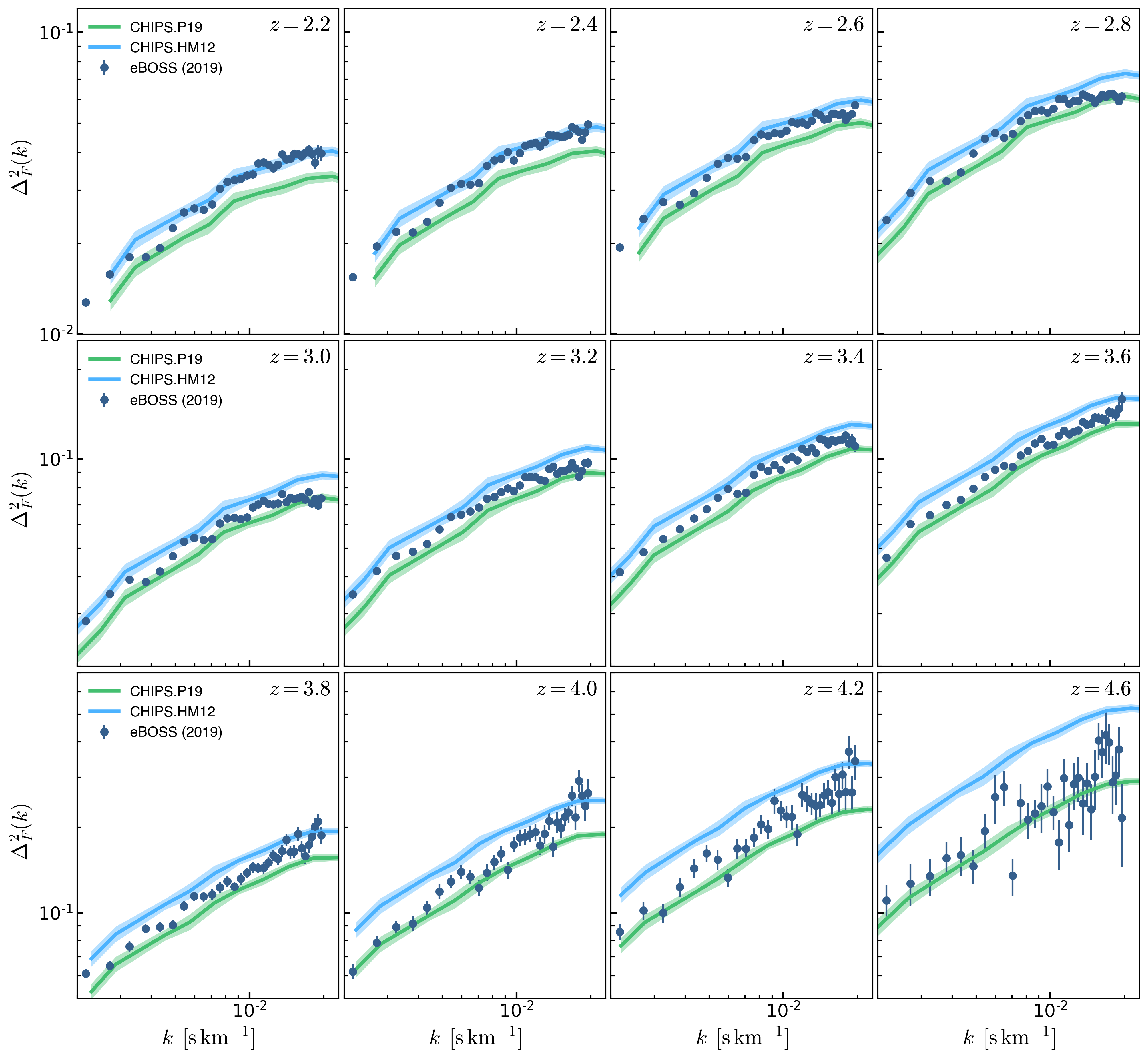
Below is the comparison to the data using \(\sigma\) from the \(N_s=5000\) bootstrap.