After adding the \(\sqrt{a}\) factor to the particles velocities., I can reproduce the optical depth of the skewers provided by Ewald. The blue lines are the Skewers that I compute and the orange lines correspond to the LOS data provided by Ewald, differences on the effective optical depth for each skewers are less than 1%

Skewer 1

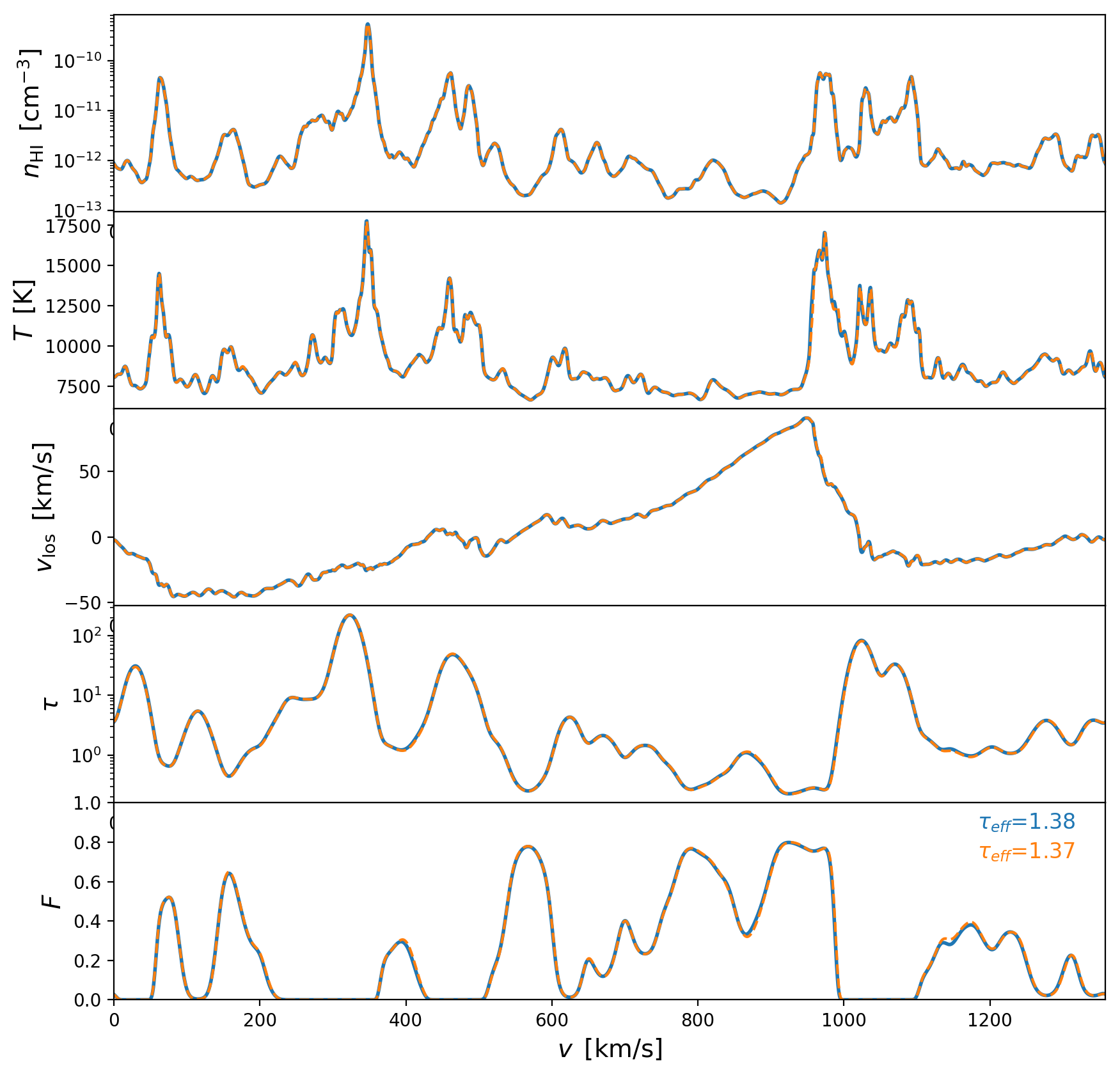
Skewer 2

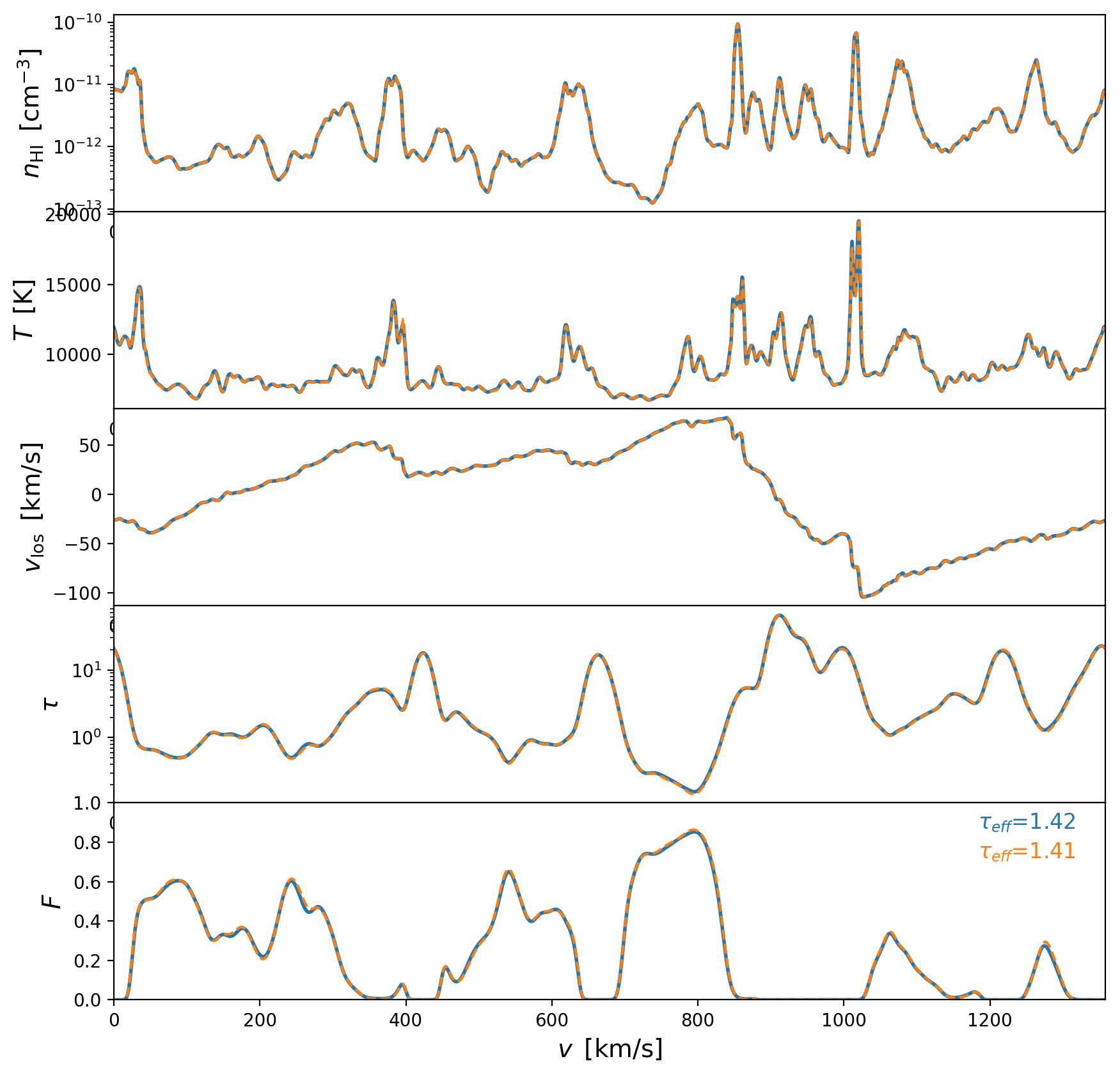
Skewer 3

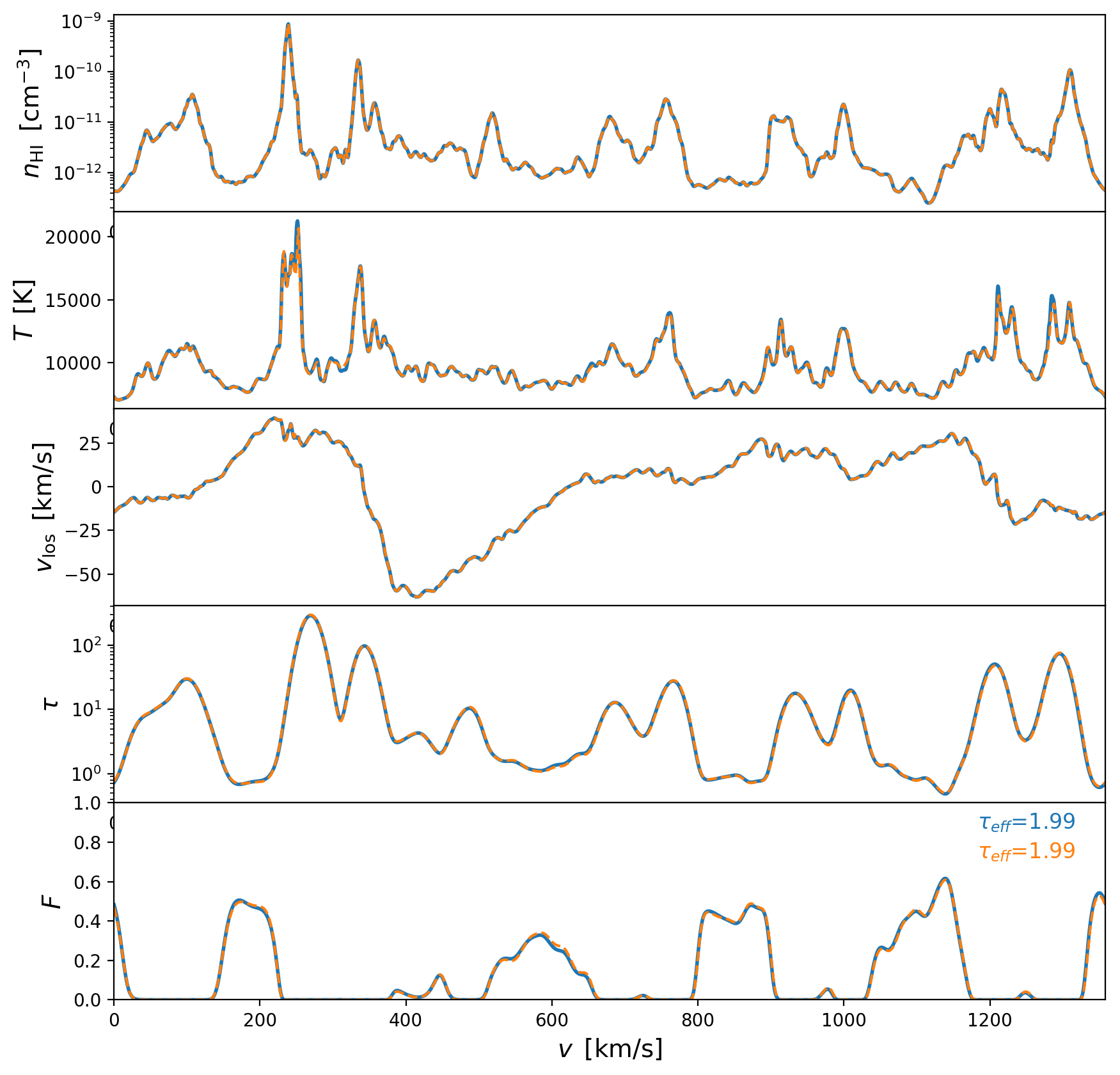
Skewer 4

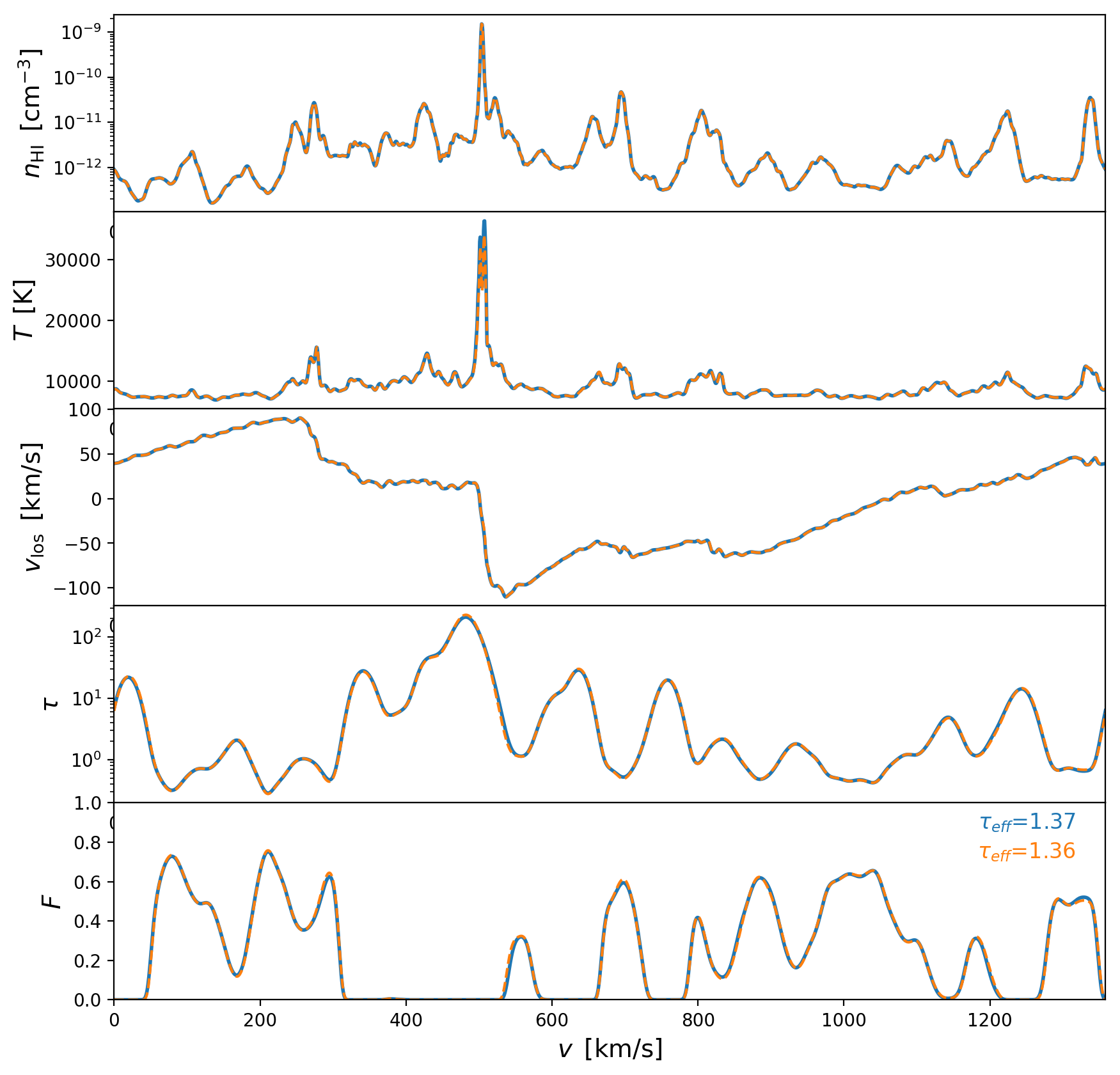
Skewer 5

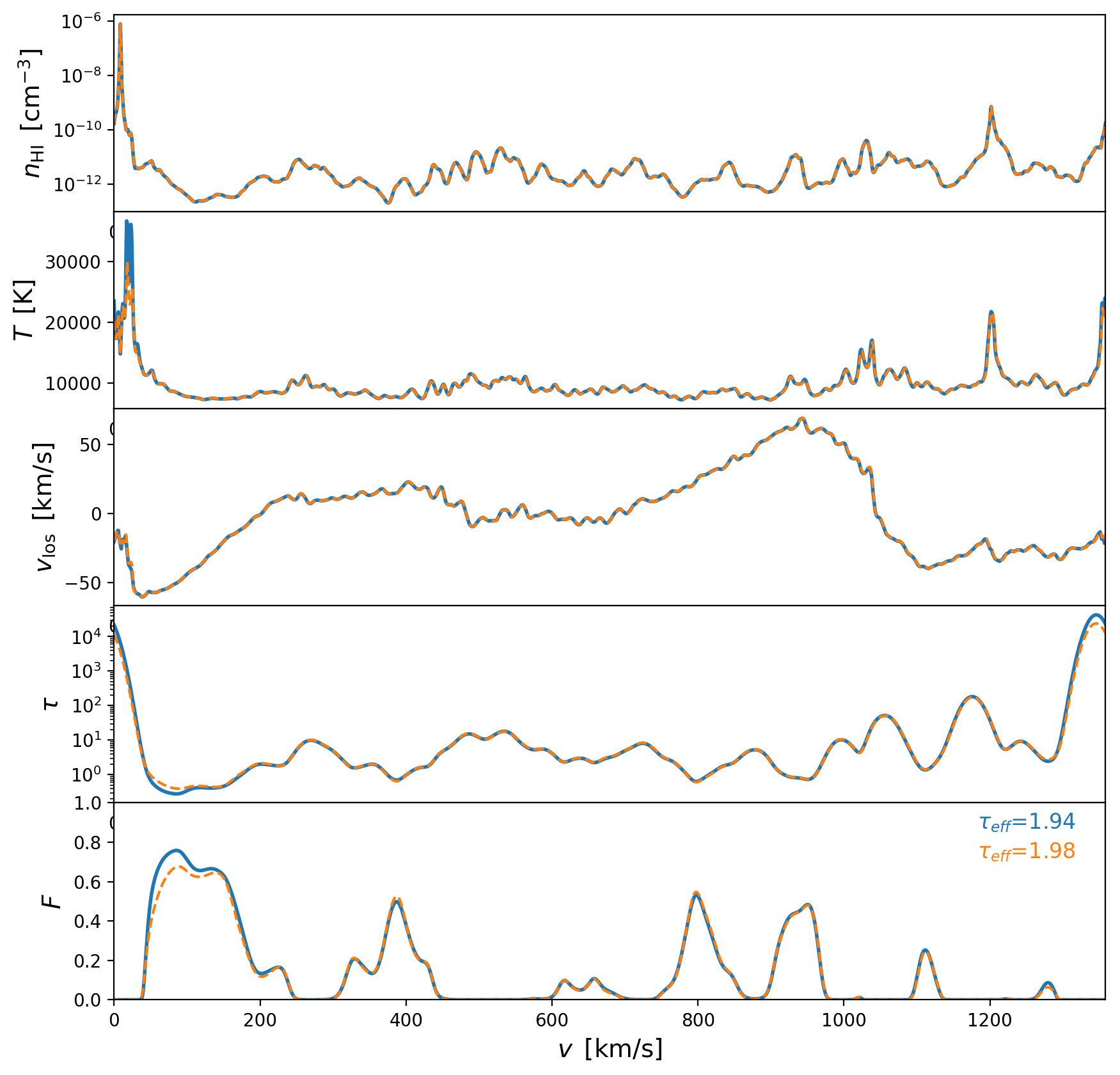
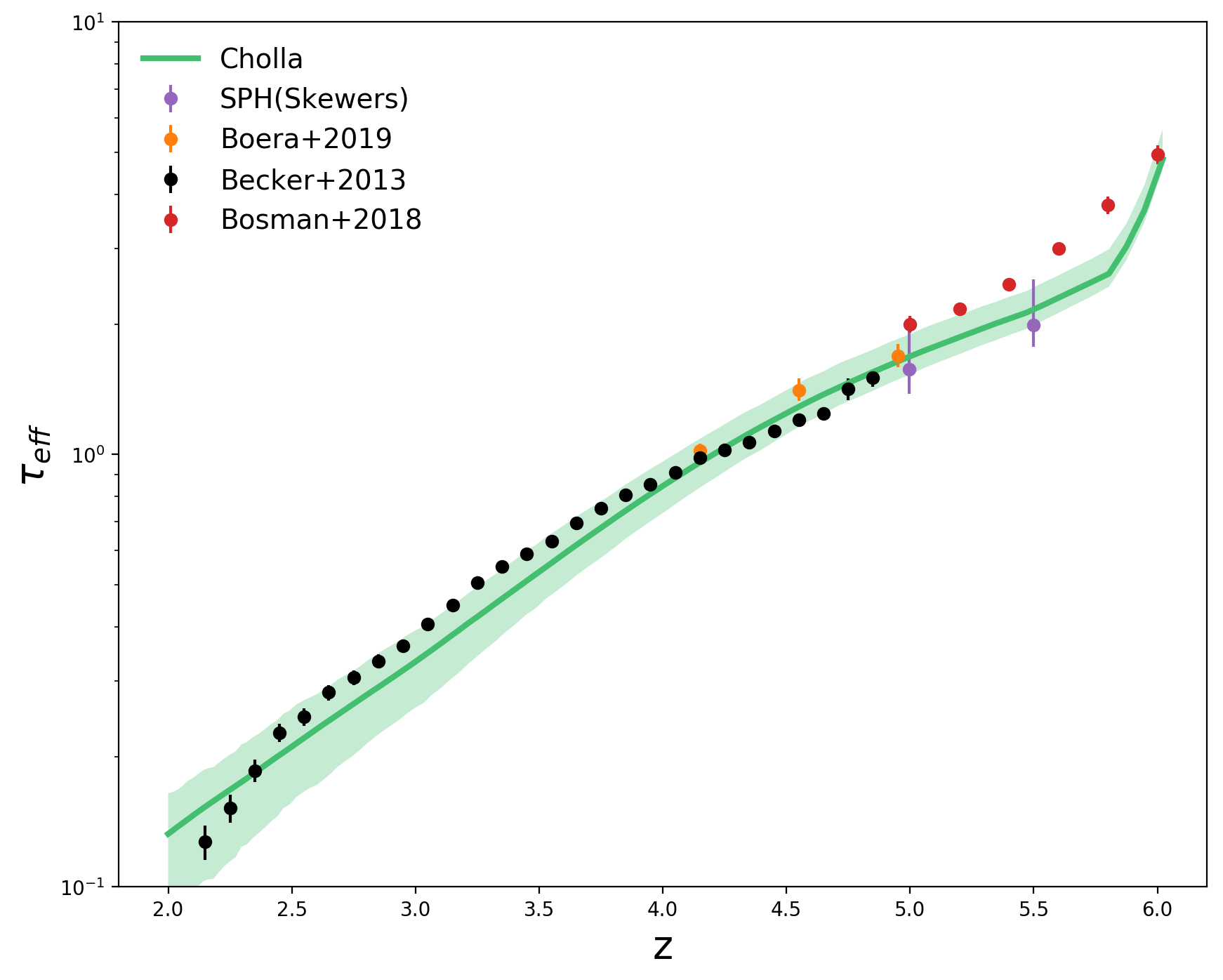
After adding the factor of \(\sqrt{a}\), the value of \(\tau_{eff}\) that I measure from the skewers computed from the SPH simulation also matches the value of \(\tau_{eff}\) reported in Puchwein etal. 2019. But after including the \(\sqrt{a}\) factor on the SPH particle velocities, then the peculiar velocities on the Cholla simulation are higher than the peculiar velocities in the SPH simulation.

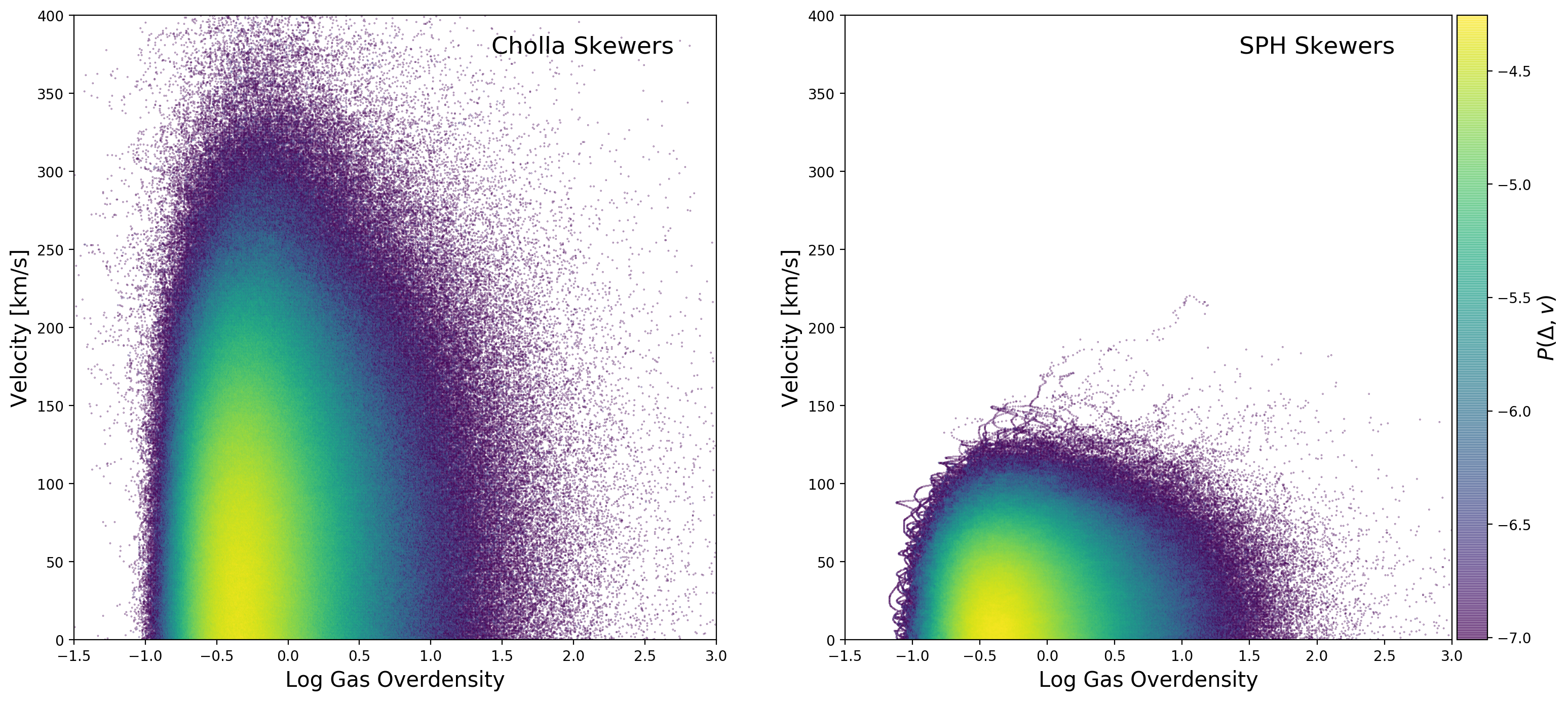
The figure below shows the Density-LOSVelocity distribution for 5000 skewers from the Cholla simulation compared to same distribution computed from 5000 skewers from the SPH simulation at z=5, the peculiar velocities of the sph skewers includes the \(\sqrt{a}\) factor.

Now if I multiply the Cholla peculiar velocities by \(\sqrt{a}\) the velocities are very similar to the SPH skewer LOS velocities, as shown in the figure below:

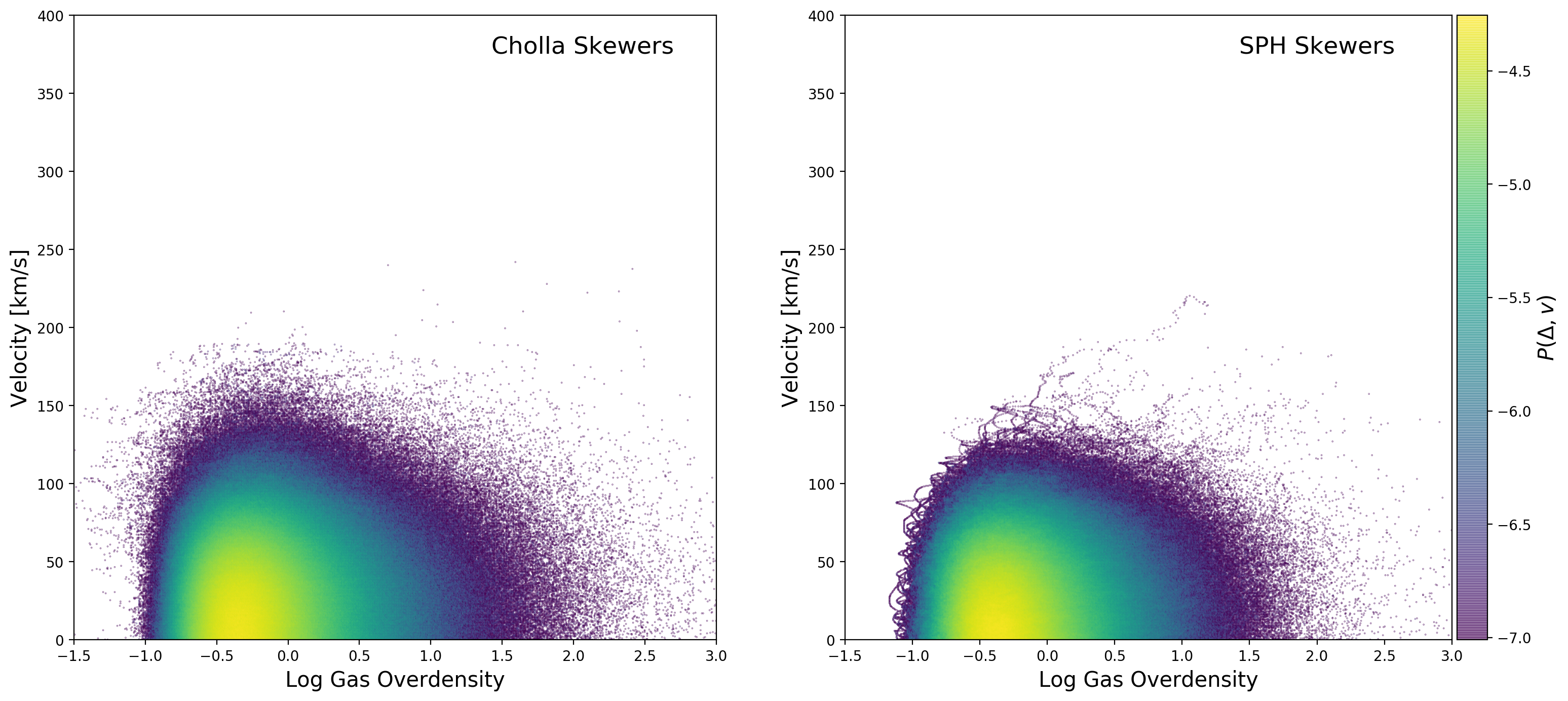
Then the question is: Am I missing a factor of \(\sqrt{a}\) when interpreting the Cholla gas peculiar velocities?

If I add the \(\sqrt{a}\) factor, the effective optical depth is shown in the figure below:

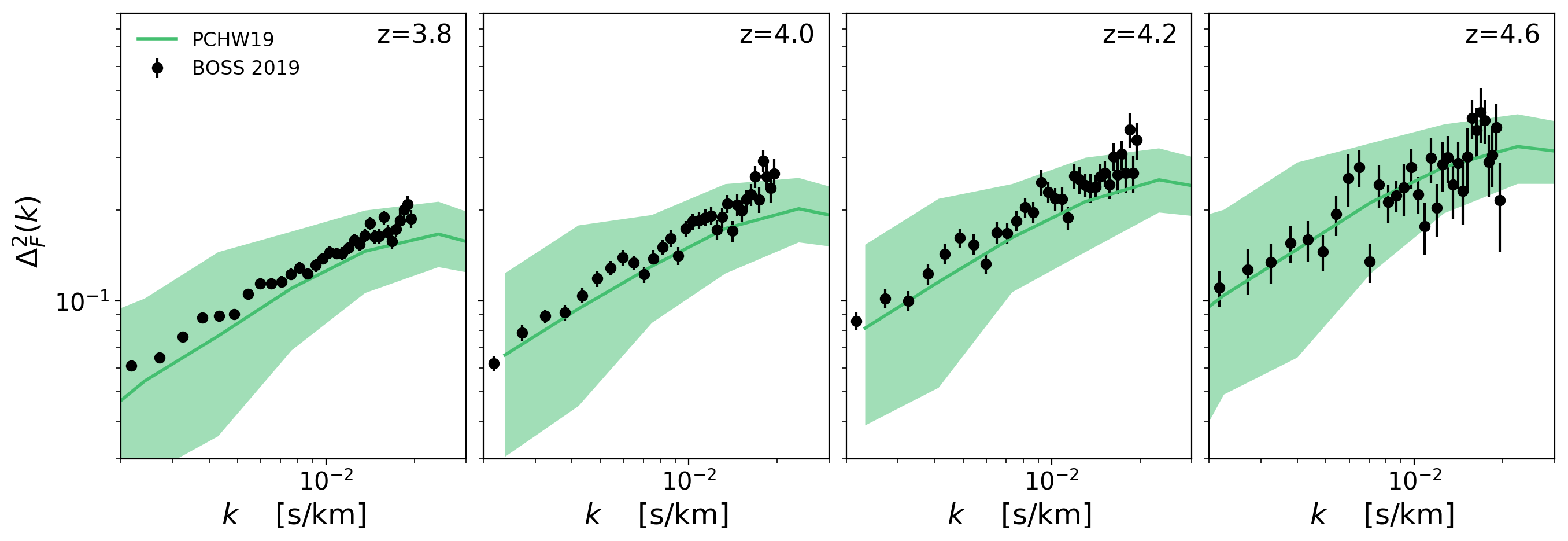
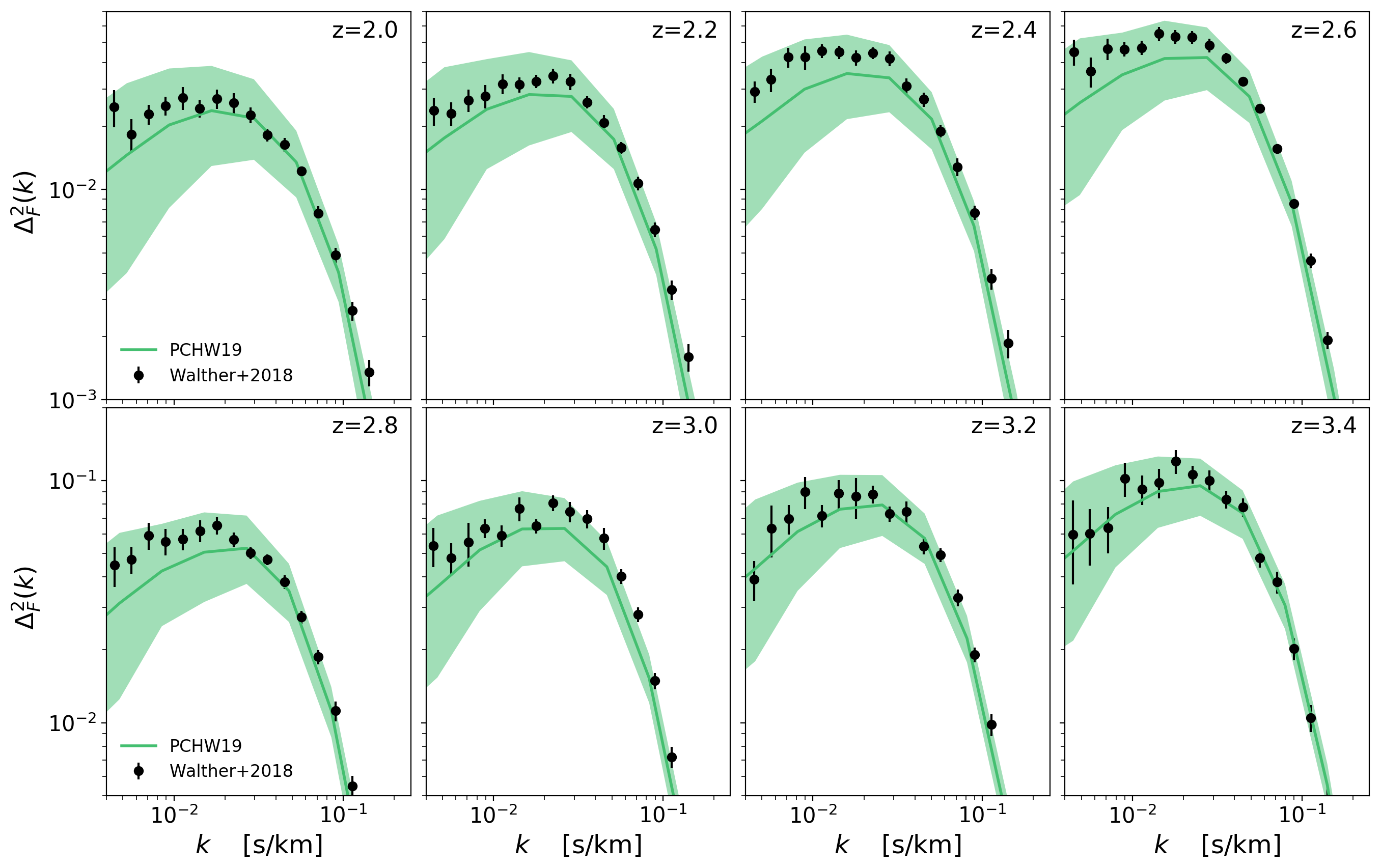
Flux Power Spectrum Small Scales:

Without \(\sqrt{a}\) factor

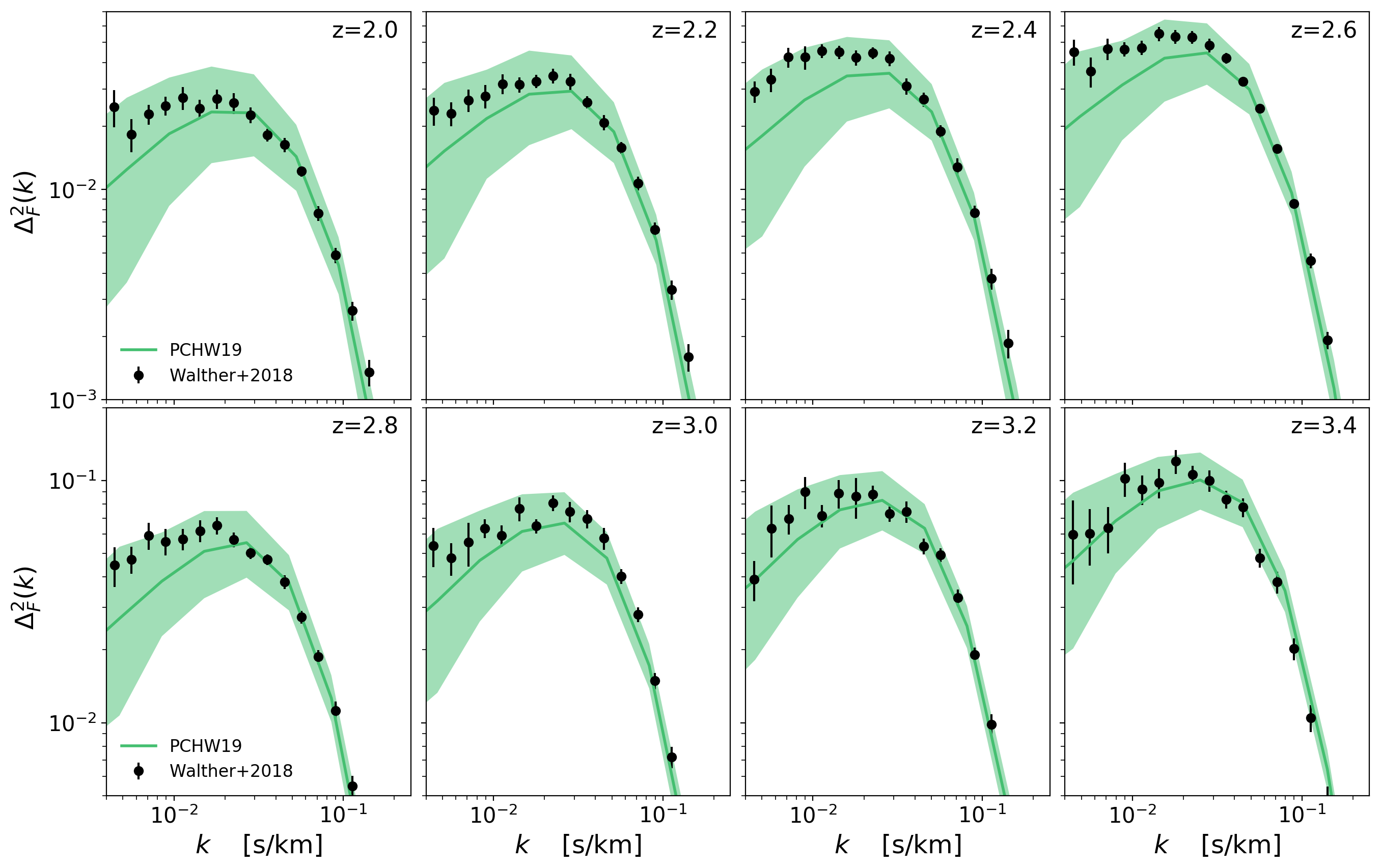
With \(\sqrt{a}\) factor

Without \(\sqrt{a}\) factor

With \(\sqrt{a}\) factor

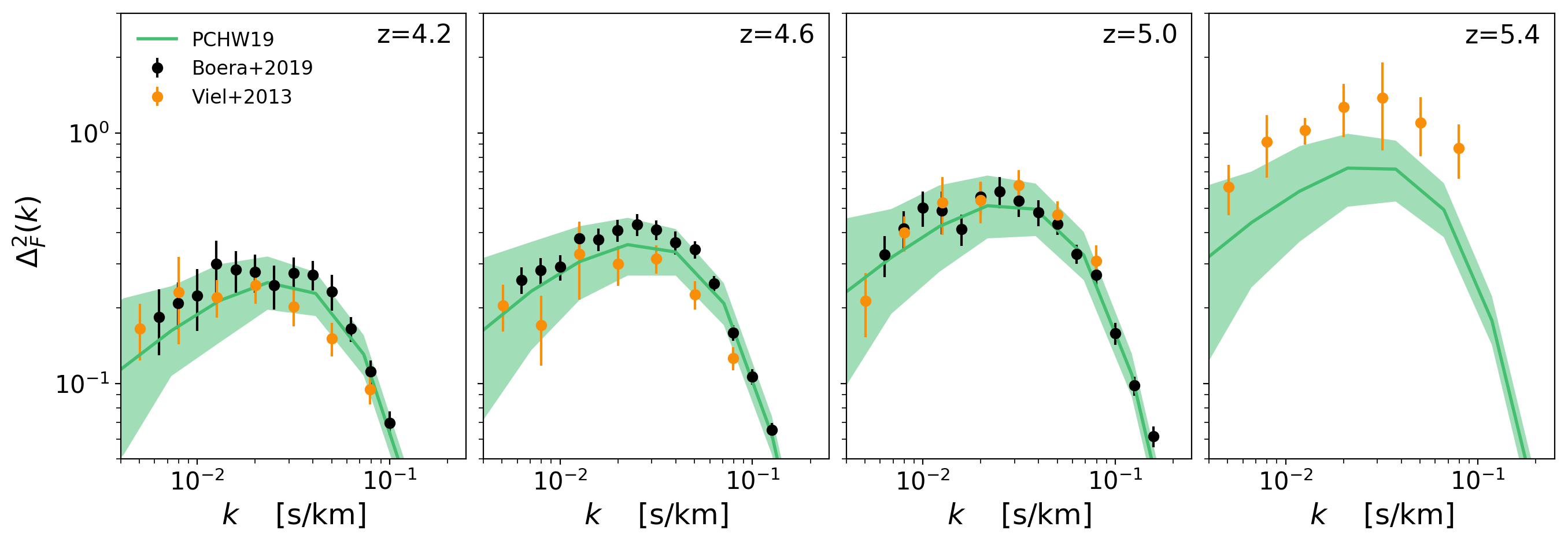
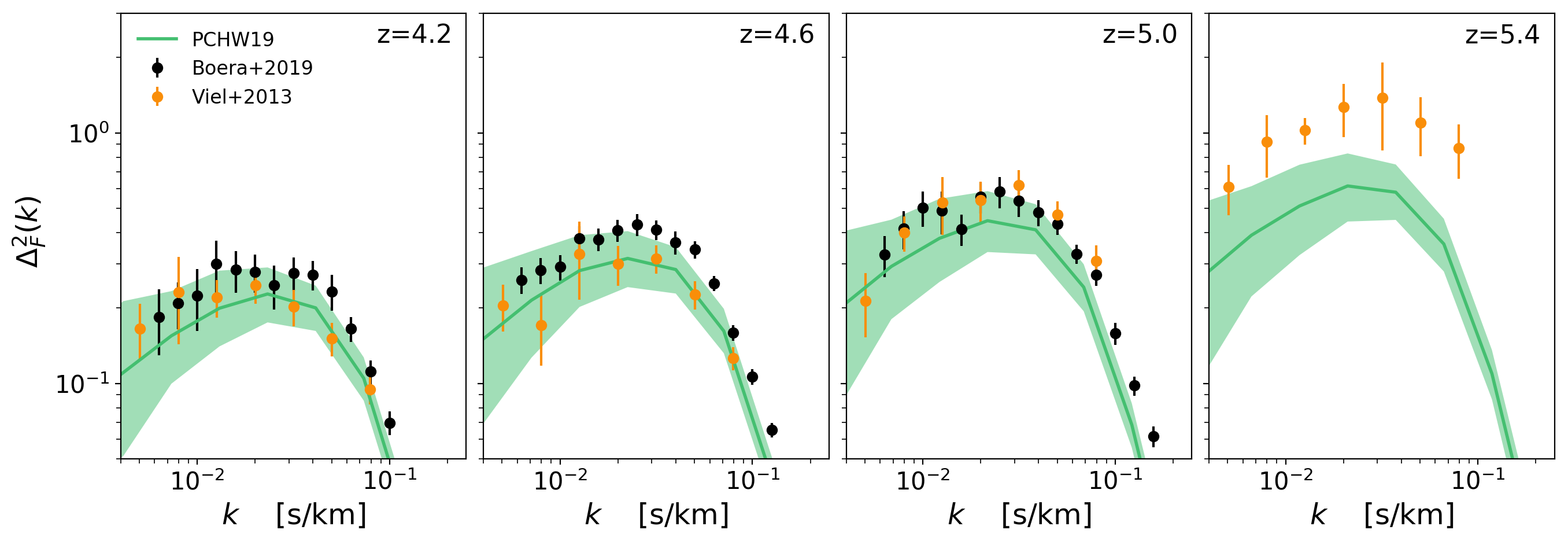
Flux Power Spectrum Large Scales:

Without \(\sqrt{a}\) factor

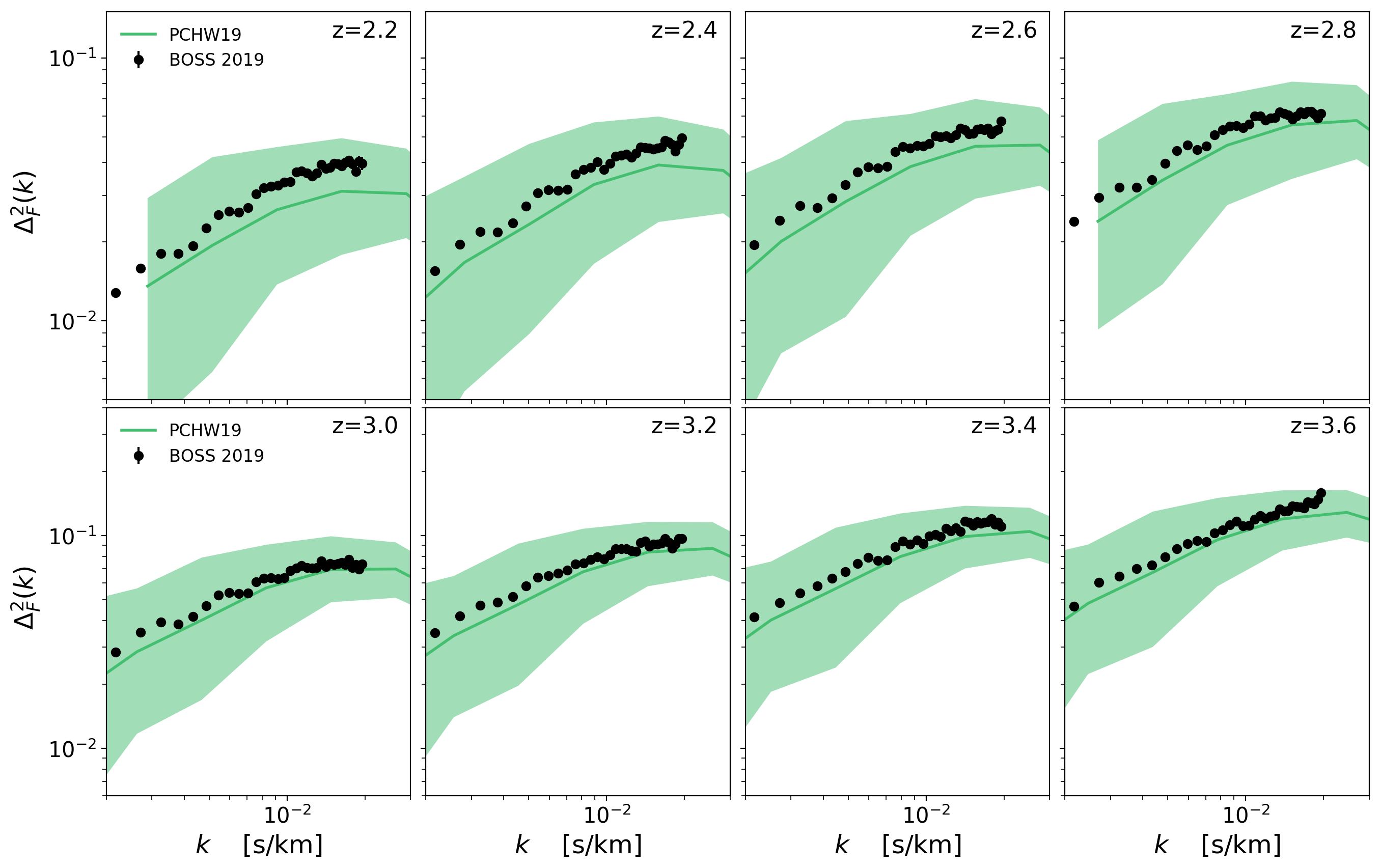
With \(\sqrt{a}\) factor

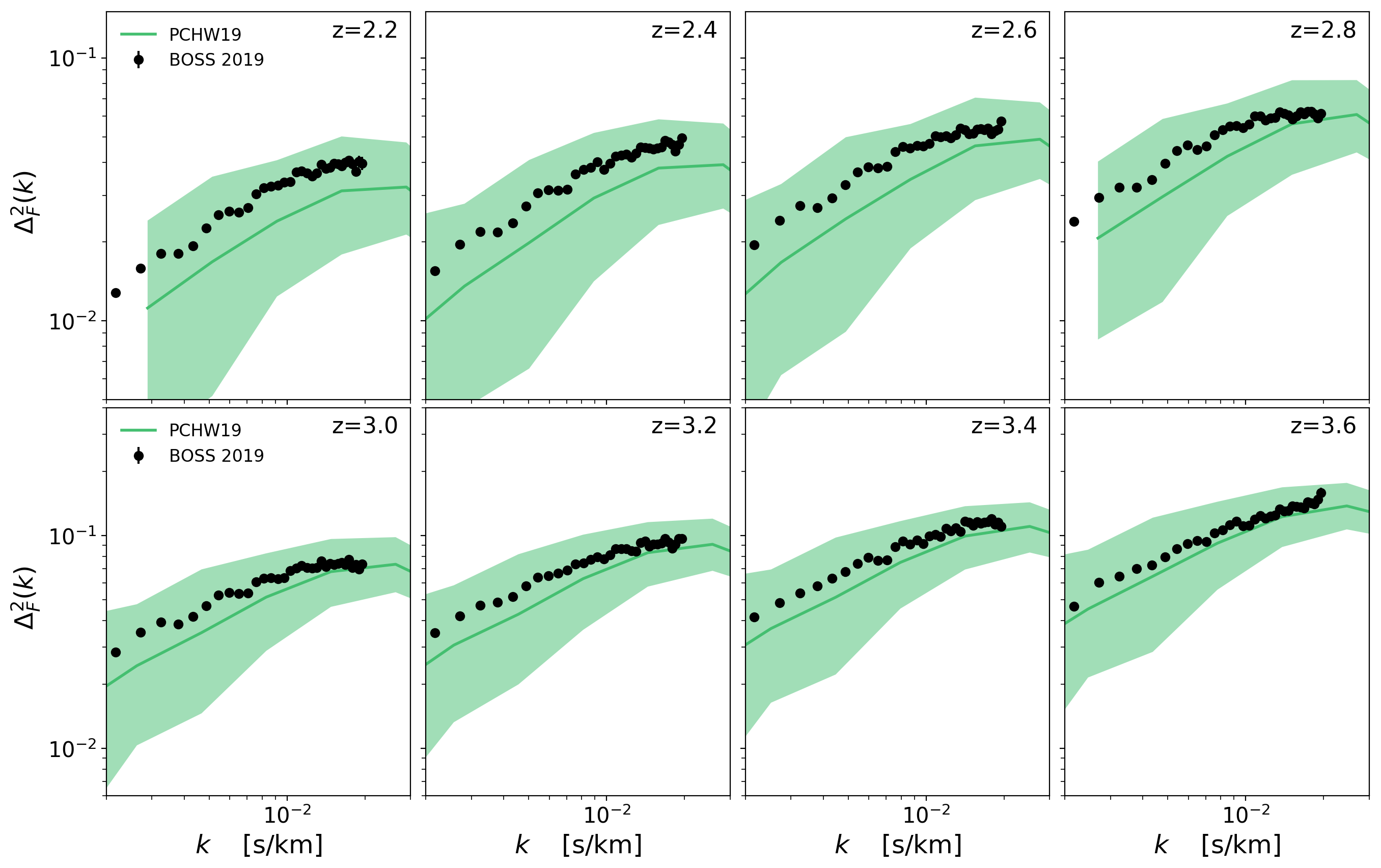
Without \(\sqrt{a}\) factor

With \(\sqrt{a}\) factor