To compare the new Poisson Solver Paris implemented by Trey White into Cholla, I ran a set of identical Dark Matter Only cosmological simulations, the parameters of the simulations are:

Box Size: 50 Mpc/h comoving

Numerical Size: 256\(^3\) dark matter particles

Cosmology: Planck 2018

NGPUs: 8

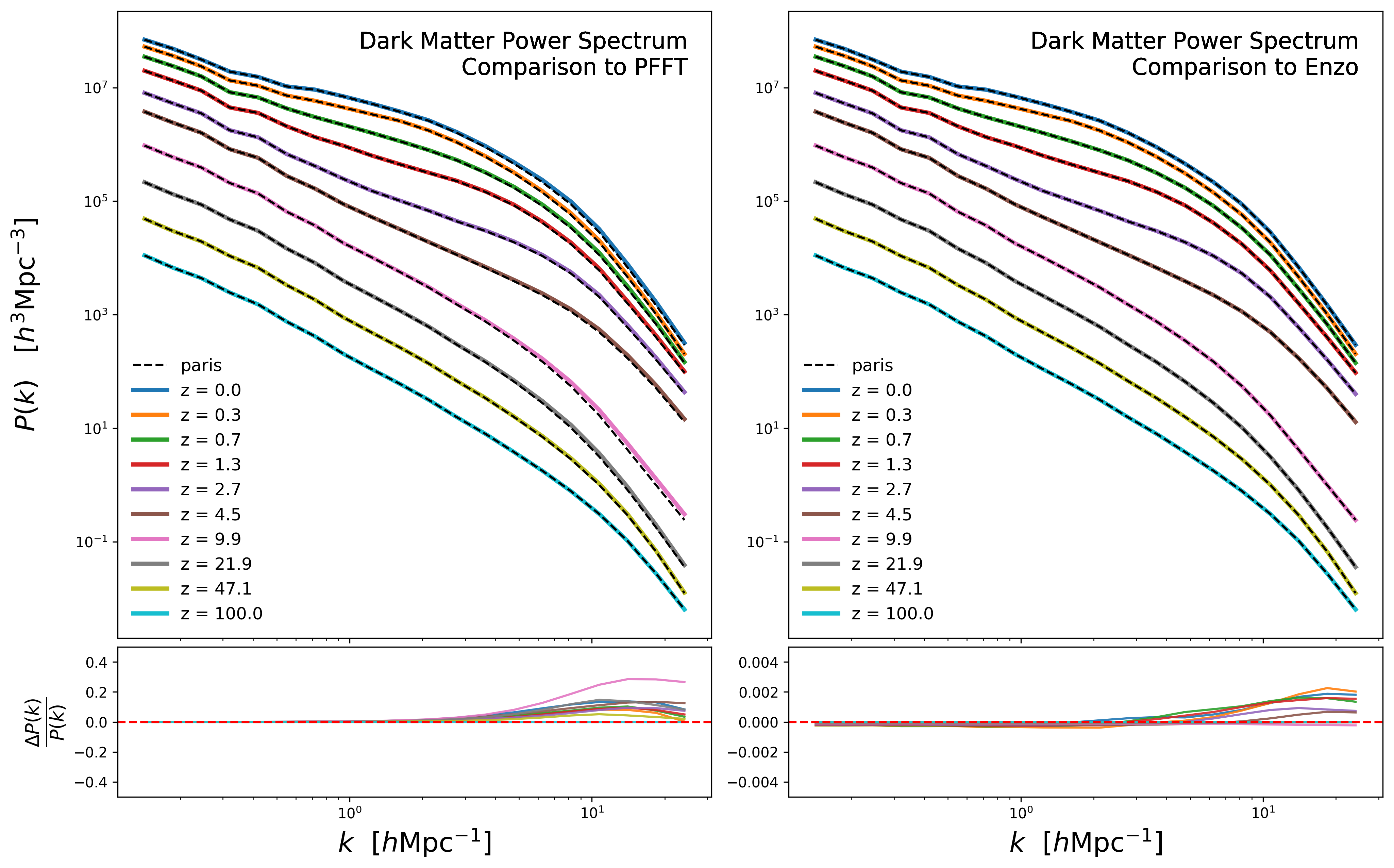
For the comparison I measured the power spectrum of the dark matter density fluctuations for several snapshots at different times (redshifts, \(z\)), the simulations start at \(z=100\) and end at the \(z=0\). The figure below shows the evolution of the powers spectrum, the panels from the left correspond to the PFFT-Solver simulation ( colored lines ) compared to the Paris-Solver simulation ( dashed lines ), the fractional differences on the power spectrum are shown in the lower panel, at small scales ( large \(k\) ) the differences are significantly large reaching as much as 25%.

We have seen these kind of differences before when comparing to the same simulations evolved with the Enzo code, so I compared the power spectrum from the Paris simulation to an analogous Enzo simulation ( plotted in the right panel ) and the differences are less than 0.5%, this explains why we were able to match the power spectrum from other codes ( Nyx and Ramses ) to less than 1% differences but not the Enzo power spectrum, it must be way the Poisson equation is solved by the different codes.

In terms of performance in my tests the Paris solver was ~2x faster than the PFFT solver.

Here is the comparison of the solution for PFFT and Paris solvers for the same simulation but solved with a lower resolution: 128\(^3\) dark matter particles, the differences appear to be similar as the 256\(^3\) simulation.