Here I explore the effect of increasing the Doppler parameter \(b\) because of turbulent velocities simply by multiplying the thermal Doppler parameter by a factor to include a turbulence boost, this is expressed as:

\[b = b_{\mathrm{thermal}} \times ( 1 + t_{boost} )\]

I measure the Transmitted Fluxes for all the skewers at z=5 (in redshift space), the figure below shows the distribution for different values of \(t_{boost}\)

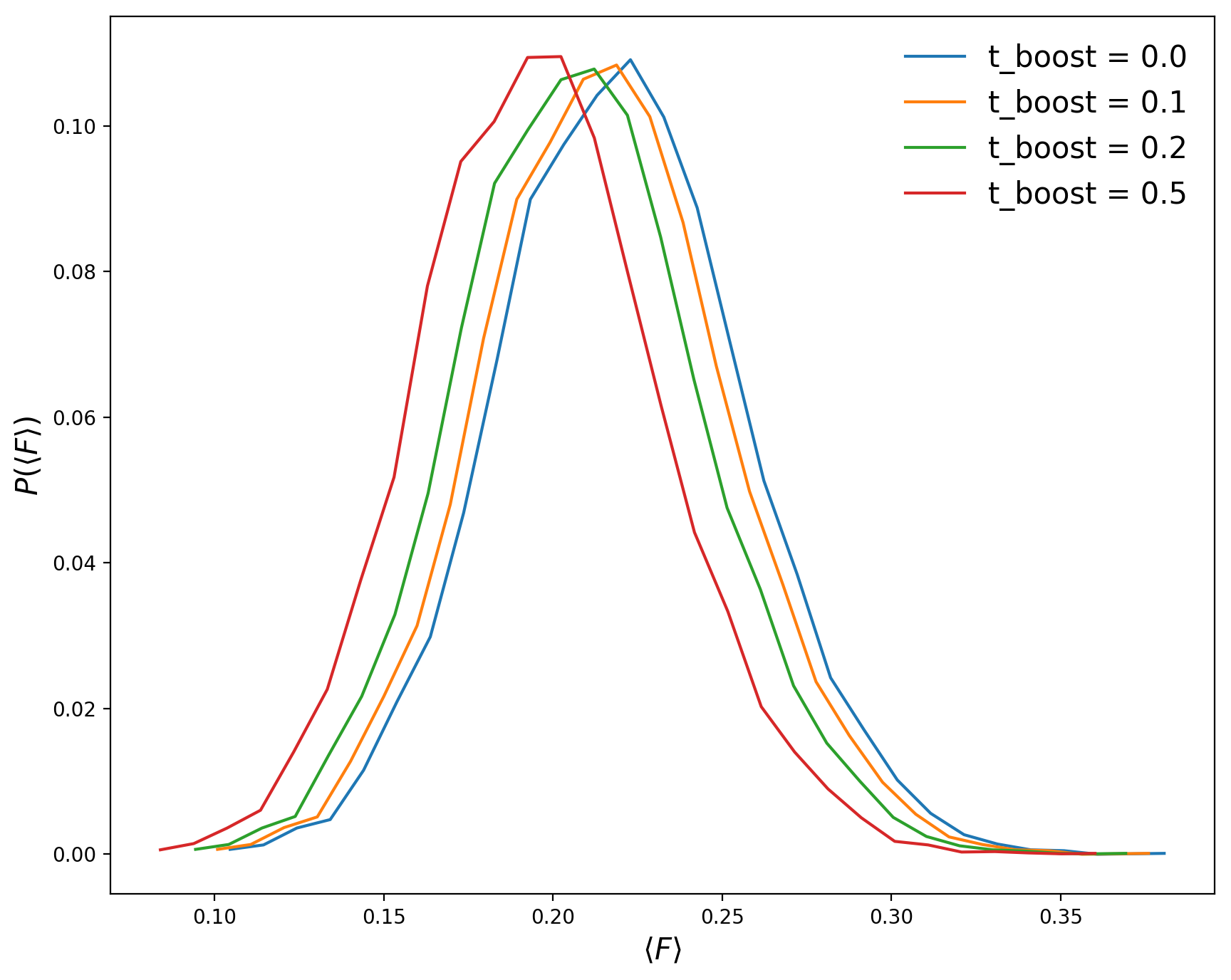
Computing the Effective Optical Depth \(\tau_{eff}\) from the average Transmitted Flux over all the skewers, I obtain the following numerical values:

\[\tau_{eff}(t_{boost} = 0.0 ) = 1.51\] \[\tau_{eff}(t_{boost} = 0.1 ) = 1.54\] \[\tau_{eff}(t_{boost} = 0.25 ) = 1.57\] \[\tau_{eff}(t_{boost} = 0.5 ) = 1.63\]

There is an increase in the Effective Optical Depth but it’s not that significant even for \(t_{boost}=0.25\)

For reference here are some values of the thermal Doppler parameter for some temperatures:

\[b_{\mathrm{thermal}}(T=1\times 10^4) \approx 13 \mathrm{km/s}\] \[b_{\mathrm{thermal}}(T=5\times 10^4) \approx 29 \mathrm{km/s}\] \[b_{\mathrm{thermal}}(T=1\times 10^5) \approx 41 \mathrm{km/s}\] \[b_{\mathrm{thermal}}(T=1\times 10^6) \approx 128 \mathrm{km/s}\]