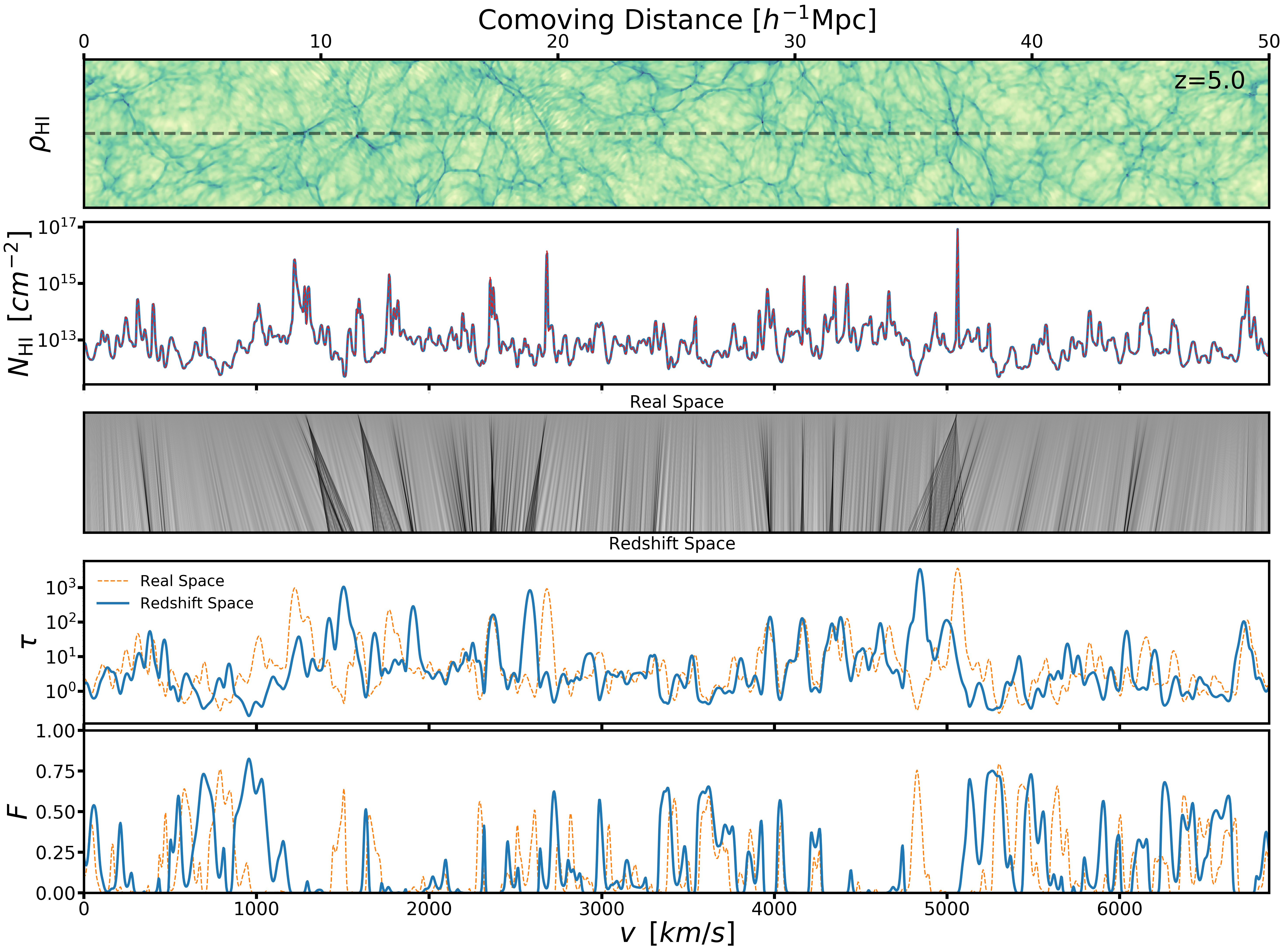
Now I compare the optical depth measured from skewers taking in to account the peculiar velocities of the gas ( redshift space ) and ignoring the peculiar velocities ( real space ).

Here I show the distribution of the average transmitted flux over each skewer and the effective optical depth computed from the average transmitted flux of each skewer at z=5.

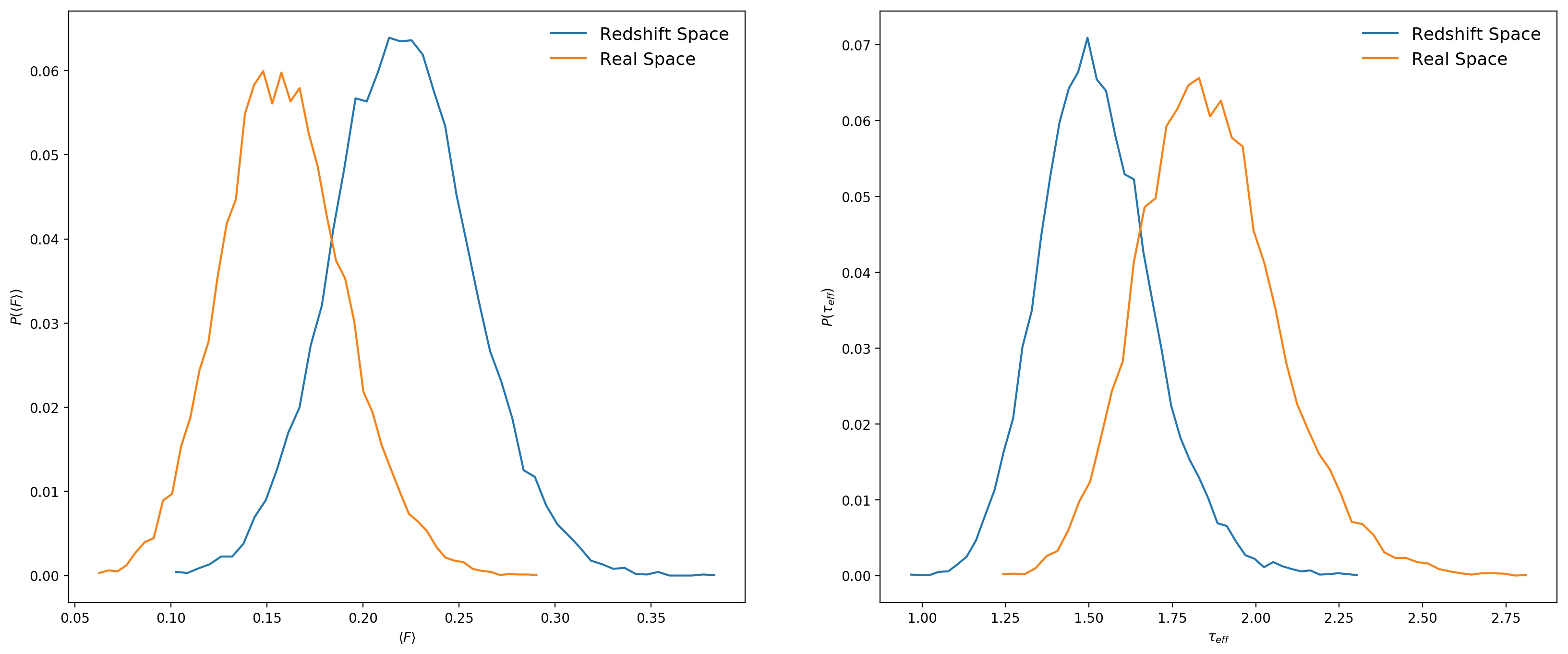
The optical depth measured in real space is higher, now lets compare as a function of redshift:

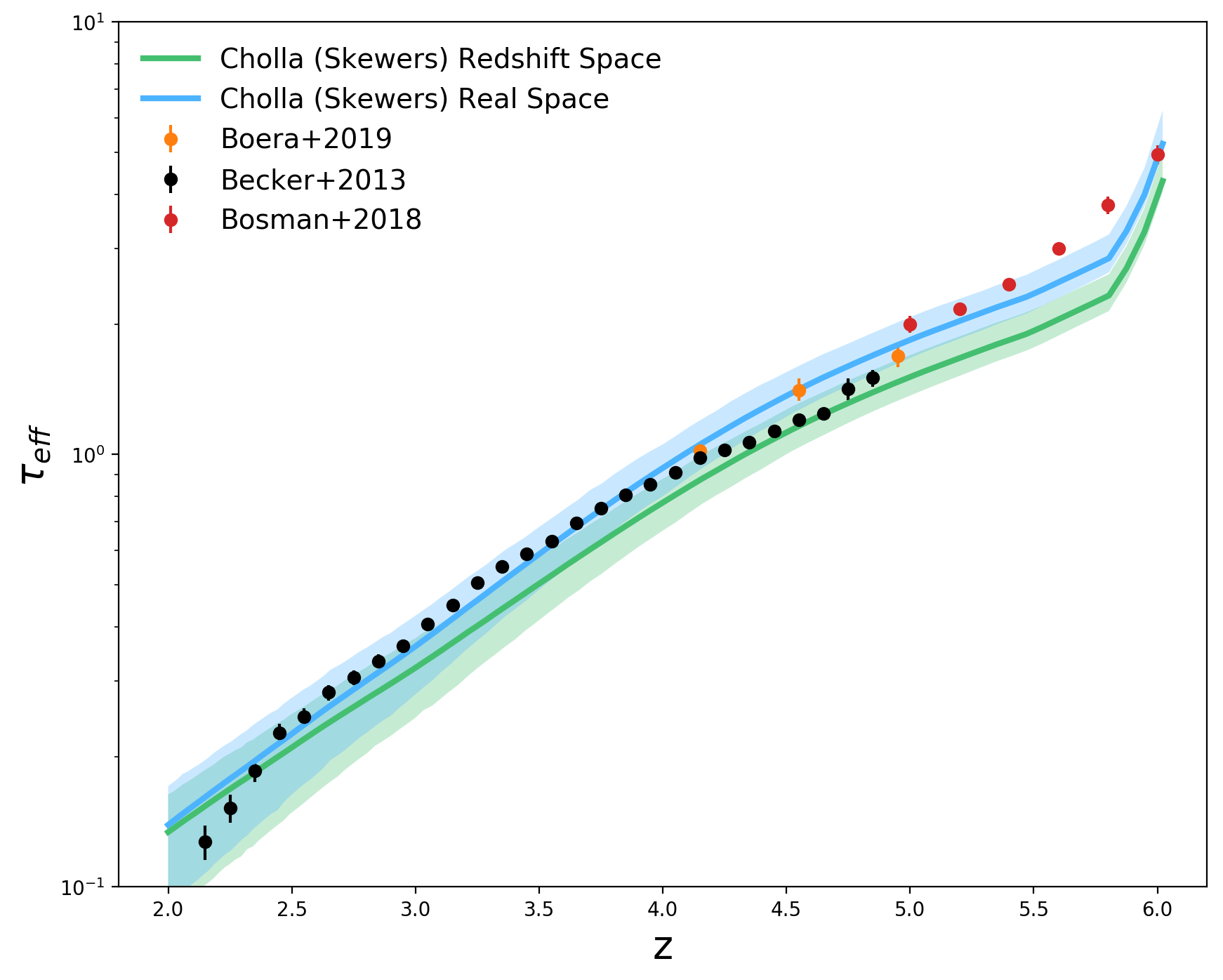
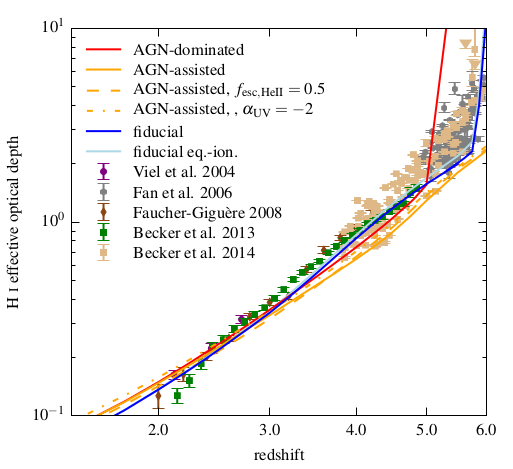
The optical depth measured in real space looks much more like the one reported by Ewald:

Here I try an experiment where i measure the mean transmitted flux due to the absorption of a single Gaussian overdensity with a uniform temperature \(T=10^4 \mathrm{K}\) and a velocity gradient across the center of the cloud

\[F_{\mathrm{diff}} = \frac{ \barF_{\mathrm{redshift}} - \barF_{\mathrm{real}}}{ \barF_{\mathrm{real}} }\]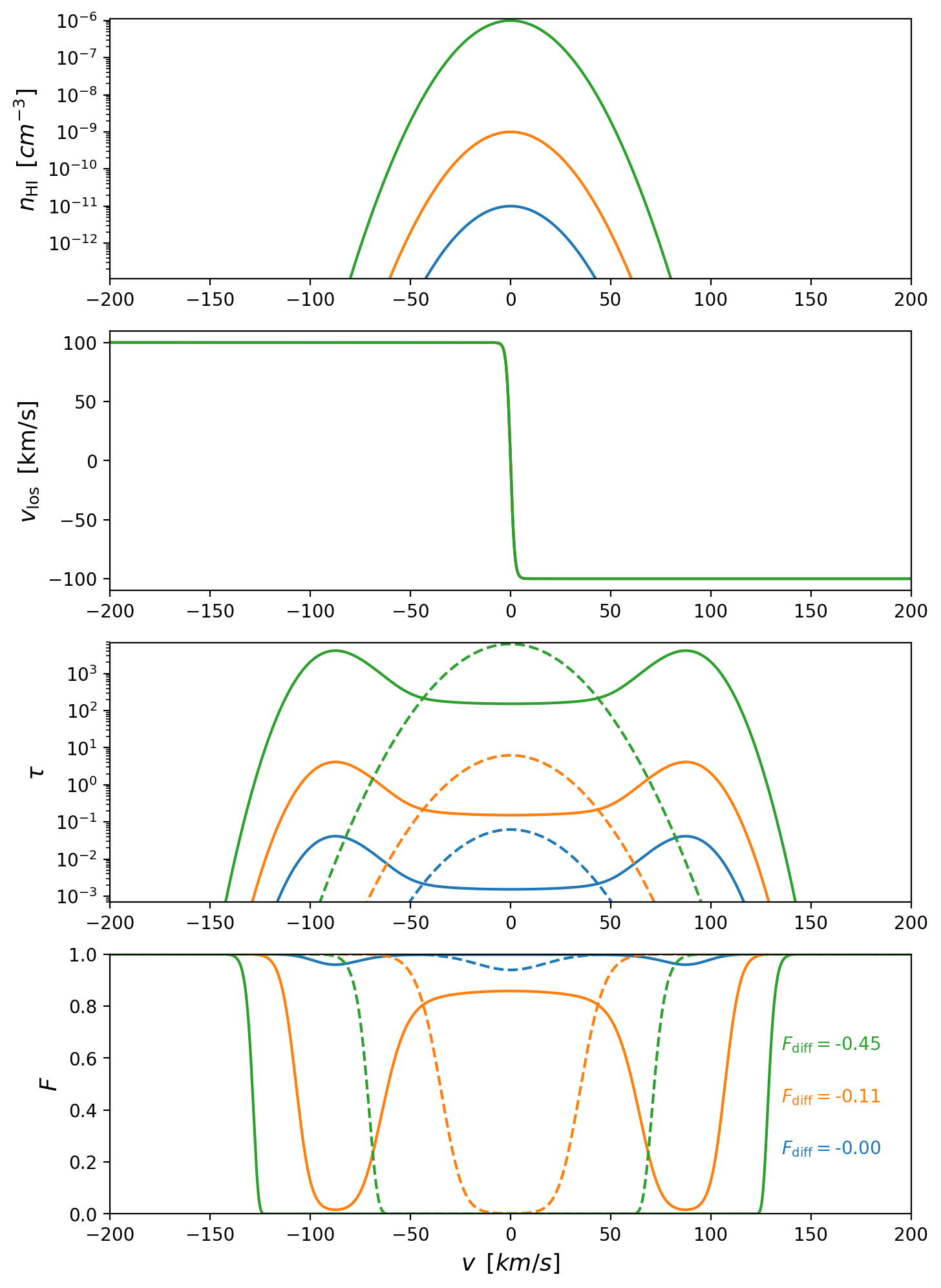

The mean transmitted flux is lower when measured in redshift space, this would imply that the optical depth is higher when measured on redshift space wich is the opposite of what I’m finding in the measurements from the simulation.