I compute the Effective Optical Depth from the full grid by averaging the transmitted flux of each cell:

\[e^{-\tau_{\mathrm{eff}}}= \frac{1}{N} \sum e^{-\tau(n_{\mathrm{HI}})}\]

where the optical depth of each cell is given by:

\[\tau(n_{\mathrm{HI}})=\frac{\pi e^{2} \lambda_0}{m_{e} c H} f_{12} n_{\mathrm{HI}}\]

Plotting the new measurement:

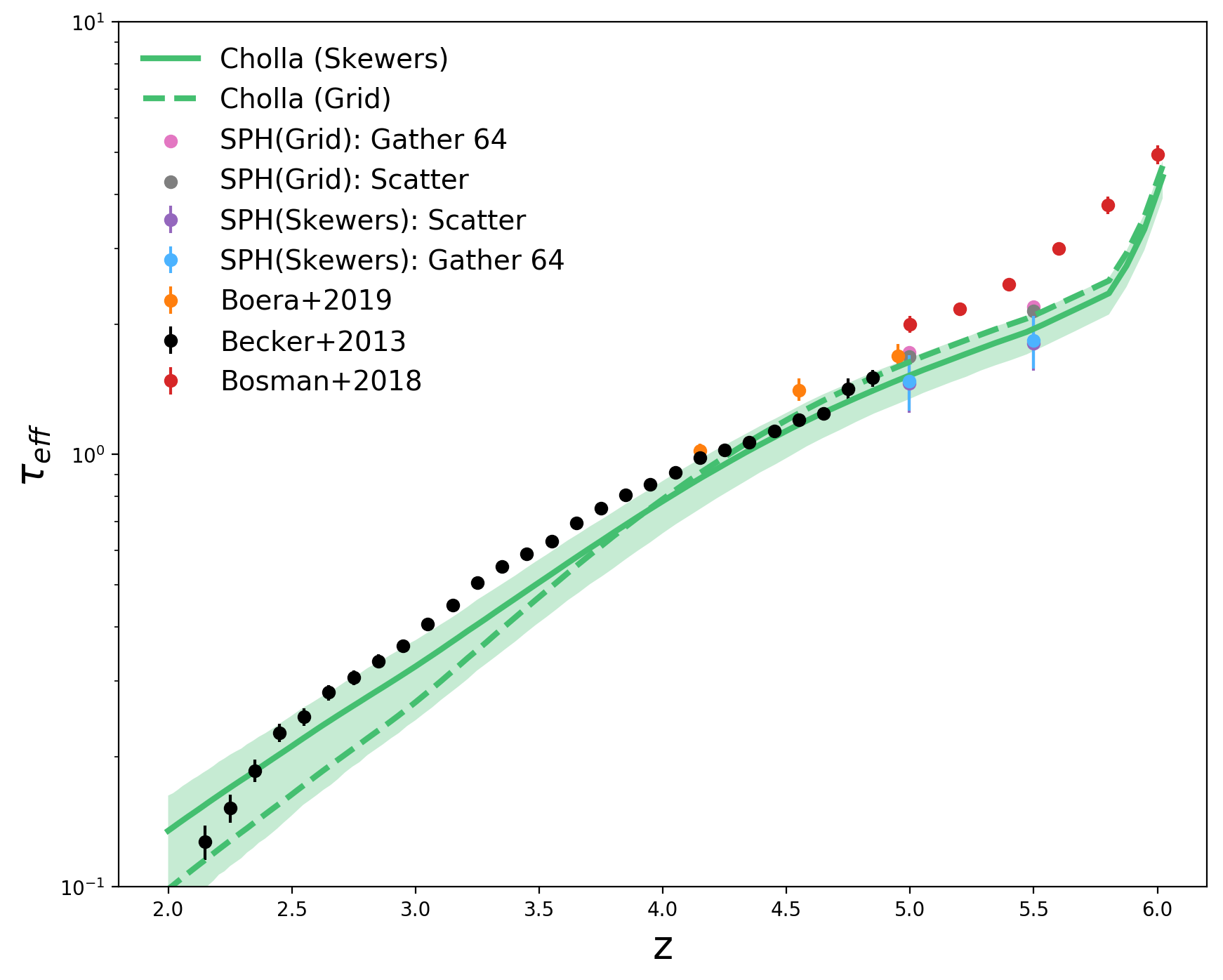
The optical depth measured from the grid is higher compared to the one measured from the skewers for z>4 but it’s lower for z<4, it’s not clear whats happening.

The Numerical values of the optical depth at z=5 and z=5.5 are:

\[\tau_{\mathrm{eff}}(z=5) \approx 1.7\] \[\tau_{\mathrm{eff}}(z=5.5) \approx 2.1\]

Comparing to the result from Puchwein et al. 2019, seems like for the new optical depths measured from the grid are consistent with the ones reported by Ewald,

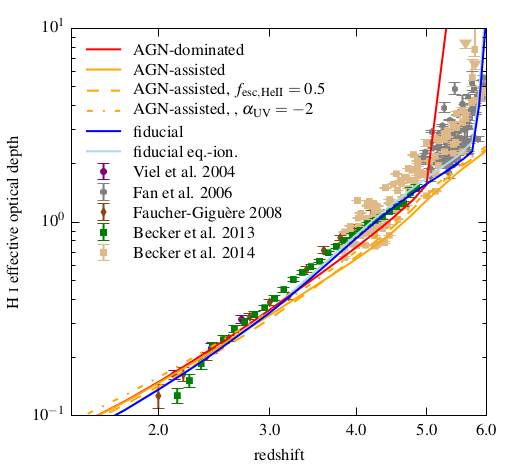
The question is: what is happening at z<4 for the optical depth measured from the grid.