Transmitted Flux Calculation
Most equations were taken from this paper: Lukic et al. 2016
The optical depth \(\tau\) for Ly\(\alpha\) scattering is given by:
\[\tau_{\nu}=\int n_{\mathrm{HI}} \sigma_{\nu} dr\]where \(\nu\) is the frequency, \(n_{\mathrm{HI}}\) is the number density of neutral hydrogen, \(\sigma_{\nu}\) is the cross section of the interaction and \(dr\) is the proper path element. Assuming a Doppler line profile, the optical depth is given by:
\[\tau_{\nu}=\frac{\pi e^{2}}{m_{e} c} f_{12} \int \frac{n_{\mathrm{HI}}}{\Delta \nu_{\mathrm{D}}} \frac{\exp \left[-\left(\frac{\nu-\nu_{0}}{\Delta \nu_{\mathrm{D}}}\right)^{2}\right]}{\sqrt{\pi}} d r\]where \(\Delta \nu_{\mathrm{D}}=(b/c)\nu_0\) is the Doppler width with the Doppler parameter due to thermal motions \(b=\sqrt{2k_bT/m_H}\), and \(f_{12}\) is the is the upward oscillator strength of the Ly\(\alpha\) resonance transition of frequency \(\nu_0\).
In the Optical depth equation they define \(\tau_{\nu}\) as an integral over \(\nu\) which I think is misused notation, I think that equation defines the optical depth at the frequency \(\nu_{\mathrm{obs}}\) which corresponds to the frequency in the frame of the observer that maps to the Ly\(\alpha\) frequency \(\nu_0\) when converted to the frame of the absorber.
Not lets think of about an specific absorber that is moving with velocity \(u_0\), if we set ourselves on the frame of the absorber, then we will see that our neighboring gas elements are are moving with respect to us with velocity \(\Delta u\)( that depends on the distance to the neighbor, ignoring peculiar velocities ), since our neighbor is moving with respect to us, then due to Doppler effect the frequency in which our neighbor will absorb is shifted with respect to our frequency of a absorption (which corresponds to \(\nu_0\) ). In the frame of the absober, the frequency of absorption of our neighbor is given by Doppler effect:
\[\nu=\nu_{0}\left(1-\frac{\Delta u}{c}\right)\]If we make a variable change from frequency to velocity in the optical depth equation and using the expansion of the universe to transform \(dr\) to \(du\) by \(du = H dr\), we obtain:
\[\tau=\frac{\pi e^{2}}{m_{e} \nu_0 H} f_{12} \int \frac{n_{\mathrm{HI}}}{b} \frac{\exp \left[-\left(\frac{\Delta u}{b}\right)^{2}\right]}{\sqrt{\pi}} d u\]where \(\Delta u = u-u_{0}\) is the relative velocity to the absorber. This can be rewritten as:
\[\tau=\frac{\pi e^{2} \lambda_0}{m_{e} c H} \frac{f_{12}}{\sqrt{\pi}} \int \frac{n_{\mathrm{HI}}}{b} \exp \left[-\left(\frac{u-u_{0}}{b}\right)^{2}\right] d u\]This will give the optical depth at the velocity coordinate of the absorber \(u_0\).
The result is that the optical depth at the position of the absorber has a contribution in absorption from the neighboring gas elements, this is because even when the neighbor is moving with respect to the absorber, due to the thermal motions of the atoms in the neighboring gas element a fraction of the neighboring gas will be at rest with respect top the absorber and this fraction of the neighbor will absorb at the same frequency as the absorber.
The way I think of the calculation is that each element of gas (cell) will generate a Gaussian shaped optical depth around its velocity coordinate that only depends on the local Neutral Hydrogen density and temperature of the absorber and then the optical depth along the line of sight is simply the sum of all the independent Gaussians from all the cells. Another way of computing the optical depth along the line of sight would be to loop over each cell and sum the Gaussian contribution from the all the neighbors along the line of sight (similar to the integral equation), this two options are equivalent, since they only differ in the order on which the sums are made.
Here is my code to generate the optical depth along the line of sight:
#Doppler Shift for the frequency
def get_nu( nu_0, v, c, z=None ):
nu = nu_0 * ( 1 - v/cgs.c )
if z != None: nu = nu_0 * ( 1 - v/cgs.c ) / ( 1 + z )
return nu
def get_Doppler_parameter( T ):
b = np.sqrt( 2* cgs.K_b / cgs.M_p * T )
return b
def get_Doppler_width( nu_0, T ):
b = get_Doppler_parameter( T )
delta_nu = b / cgs.c * nu_0
return delta_nu
#Copy ghost cells to extend periodic boundaries
def extend_periodic( arr, n_ghost):
n = len(arr)
arr_periodic = np.zeros( n + 2*n_ghost )
arr_periodic[n_ghost:n+n_ghost] = arr
arr_periodic[:n_ghost] = arr[-n_ghost:]
arr_periodic[-n_ghost:] = arr[:n_ghost]
return arr_periodic
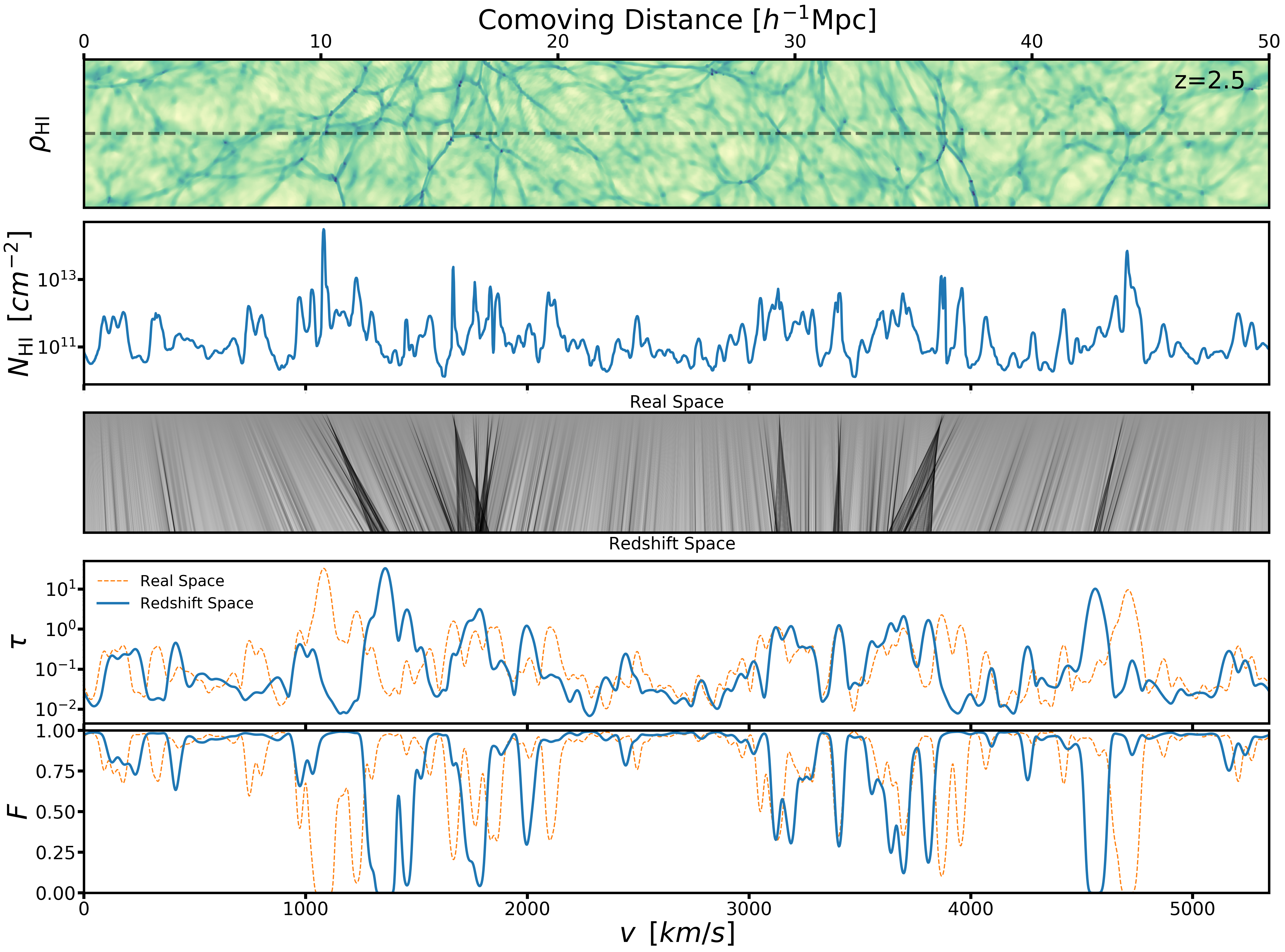
def get_optical_depth( current_z, dr, H, dv, n_HI_los, vel_Hubble_los, vel_peculiar_los, temp_los, space='redshift' ):
# Lyman Alpha Parameters
Lya_lambda = 1.21567e-5 #cm Rest wave length of the Lyman Alpha Transition
Lya_nu = cgs.c / Lya_lambda
f_12 = 0.416 #Oscillator strength
Lya_sigma = np.pi * cgs.e_charge**2 / cgs.M_e / cgs.c * f_12
H_cgs = H * 1e5 / cgs.Mpc
#Extend Ghost cells for periodic boundaries
n_ghost = 256
n_HI = extend_periodic( n_HI_los, n_ghost)
vel_peculiar = extend_periodic( vel_peculiar_los, n_ghost )
temp = extend_periodic( temp_los, n_ghost)
n = len(n_HI_los)
r_proper = np.linspace( -n_ghost, n+n_ghost-1, n+2*n_ghost)* dr
vel_Hubble = H * r_proper * 1e5
n_points = len( n_HI )
if space == 'real': velocity = vel_Hubble
if space == 'redshift': velocity = vel_Hubble + vel_peculiar
tau_los = np.zeros(n_points) #Initialize arrays of zeros for the total optical depth along the line of sight
#Loop over each cell
for i in range(n_points):
#Get local values of the cell
v_0 = velocity[i] #Velocity of the cell
n_HI_0 = n_HI[i] #HI number density of the cell
temp_0 = temp[i] #temperature of the cell
b = get_Doppler_parameter( temp_0 ) #Doppler parameter of the cell
#Compute the Gaussian component of the optical depth from this single cell
exponent = ( vel_Hubble - v_0 ) / b
phi = 1. / ( np.sqrt(np.pi) * b ) * np.exp( -1 * exponent**2 )
tau = Lya_sigma * Lya_lambda / H_cgs * n_HI_0 * phi * dv
#Add the Gaussian component from this cell to the global optical depth along the line of sight
tau_los += tau
# Trim the ghost cells from the global optical depth
tau_los = tau_los[n_ghost:-n_ghost]
return tau_los
To compute \(\tau_{eff}\) there are two ways that I can think of:
-
Compute the \(\tau_{mean}\) along each skewer and then average over all skewers.
-
Compute \(F_{mean}\) along each skewer, then average over all skewers and then compute \(\tau_{eff} = - \mathrm{log} \langle F \rangle\). I think this is the correct way.
I compared both ways of doing it and the differences are less than 2%.