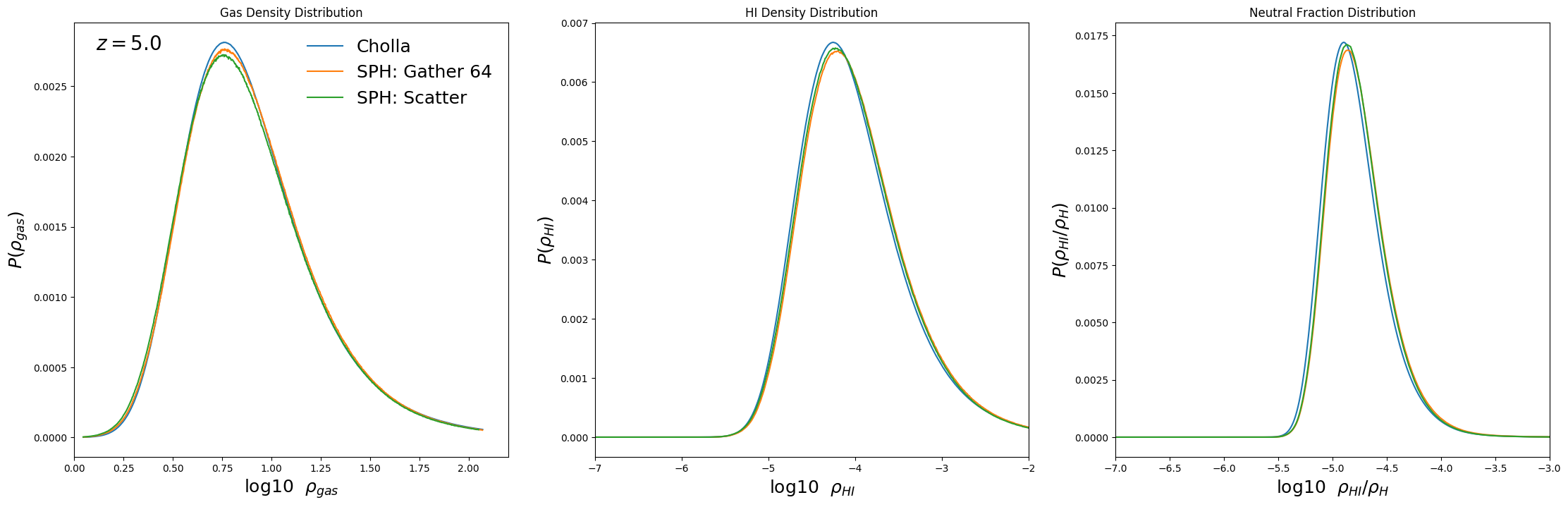
Density Distributions ( z = 5 )

On my previous post I found that there was more Neutral Hydrogen on the SPH(Grid) compared to the HI distribution on the Cholla simulation. After some thought I realized that the way I was doing the HI density interppolation onto the grid was not correct.

I Think that the correct way to do the interpolation is given by the following equation:

\[\rho_{HI,i}=\sum_{j=1}^{N} m_{HI,j} W_j\]

where \(m_{HI,j} = HI_j * X * m_j\) and \(HI_j\) is the neutral hydrogen fraction from the Gadget file, \(X=0.759\) is the hydrogen fraction and \(m_j\) is the particle mass from the Gadget file.

After interpolating again the Neutral Hydrogen density onto the \(512^3\) grid using the above equation, the distribution of Neutral Hydrogen on the SPH(Grid) is much closer to the one measured on the Cholla simulation.

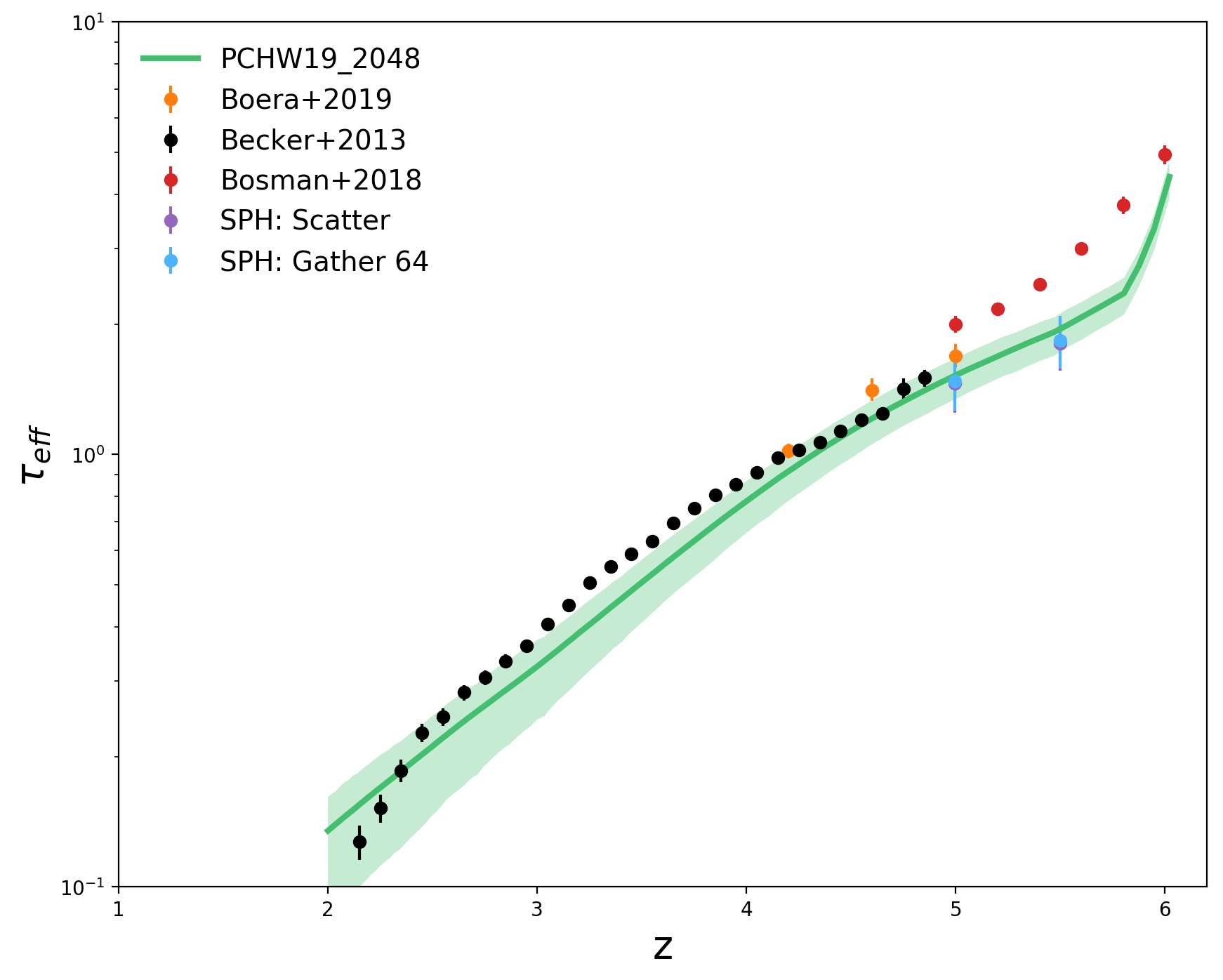
Optical Depth Comparison

After computing the optical depth from the new HI distribution, the optical depth that I measure on the SPH(Grid) is slightly lower than the one on the Cholla simulation but both seem consistent.